PyTorch 教程-PyTorch 中的梯度下降

我们最大的问题是，如何训练模型以确定将最小化我们的误差函数的权重参数。让我们开始了解梯度下降如何帮助我们训练我们的模型。

首先，线性模型将以随机的初始参数开始，回想一下当我们用线性函数初始化模型时，它确实给了我们一个随机的初始参数。

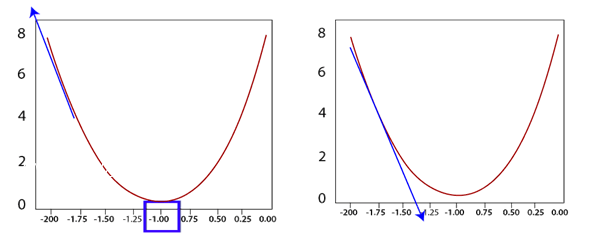
现在让我们暂时忽略偏差值，基于这个初始参数 A 关联的误差。我们的目标是向给我们较小误差的方向移动。

如果我们取误差函数的梯度，即在我们所遇到的当前值的切线斜率的导数，这个导数将引导我们向最高误差的方向移动。

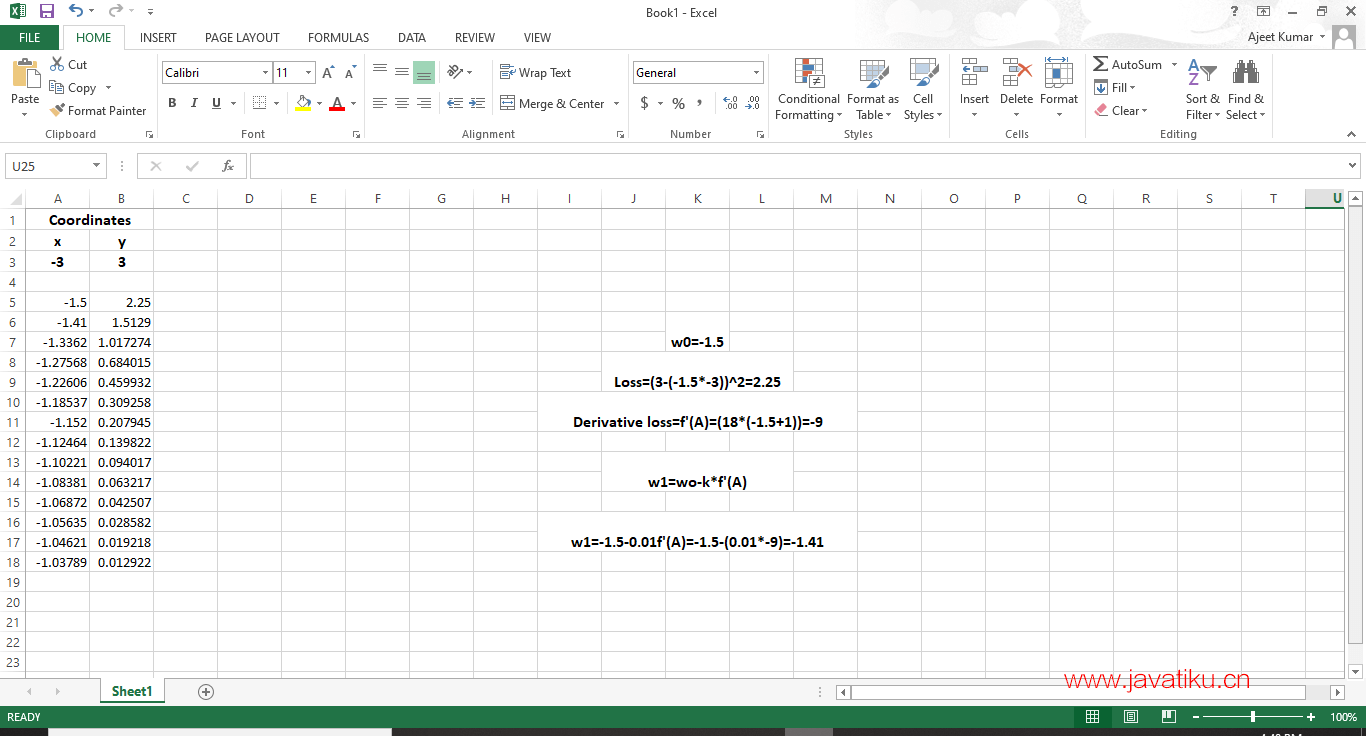
Loss=(3+3A)2
f' (A)=18(A+1)

因此，我们向梯度的负方向移动，这将引导我们向最小误差的方向移动。我们取当前的权重，并减去在同一点上该函数的导数。

A1=A0-f'(A)  

这将引导我们向最小误差的方向移动。

简而言之，首先，我们必须计算损失函数的导数，然后将其添加到线的当前权重值中。无论权重值是什么，它们都会给你梯度值。这个梯度值然后从当前权重 A0 中减去，以得到新的更新权重 A1。新的权重应该导致比之前更小的误差。我们将迭代地做这个，直到我们获得我们的线模型拟合数据的最佳参数。

我们正在沿着梯度下降，然而，为了确保最佳结果，应该以最小的步骤下降。因此，我们将梯度乘以一个称为学习率的最小数值。学习率的值是经验性的。尽管一个好的标准起始值倾向于是十分之一或百分之一，学习率需要足够小，因为随着线调整自己，你永远不希望它在一个方向上剧烈移动，因为那会导致不希望的发散行为。

在这里，我们将学习基于经验结果调整学习率，并且稍后将在代码中编写梯度下降算法，但继续我们的梯度下降示例，让我们参考 Excel 上的演示，以可视化梯度下降的效果。

我们稍后将在我们的代码中实现它。