PyTorch 教程-PyTorch 中的损失函数

在之前的主题中，我们看到线并没有正确地拟合我们的数据。为了使其最佳拟合，我们将使用梯度下降法更新其参数，但在此之前，需要了解损失函数。

因此，我们的目标是找到一条线的参数，使其能够很好地拟合这些数据。在我们之前的示例中，线性函数最初会为我们的线随机分配权重和偏差参数，如下图所示。

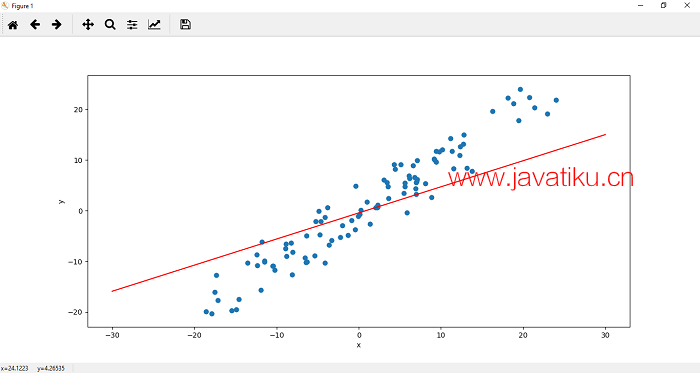
这条线并没有很好地代表我们的数据。我们需要一种优化算法，根据总误差调整这些参数，直到我们得到一条包含合适参数的线。

那么，我们如何确定这些参数呢？

为了更好地理解，我们将讨论限制在单个数据点上。

通过从该点的实际 y 值中减去预测值来确定误差。

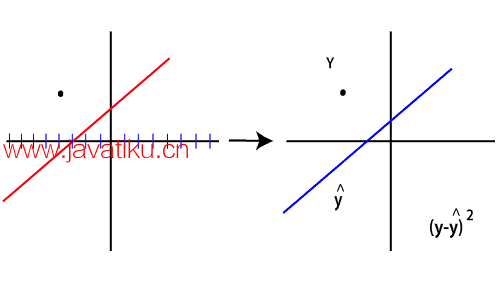
预测值越接近实际值，误差就越小。正如你已经知道的，预测可以写成：

Ax1+b

但是，我们只处理一个点。因此可以通过它画出无数条线。为此，我们先去掉偏差。现在暂时移除这个额外的自由度，并通过将偏差值固定为零来取消它。

(y-y^)2
(y-(Ax+b))2
(y-(Ax+0))2
(y-Ax)2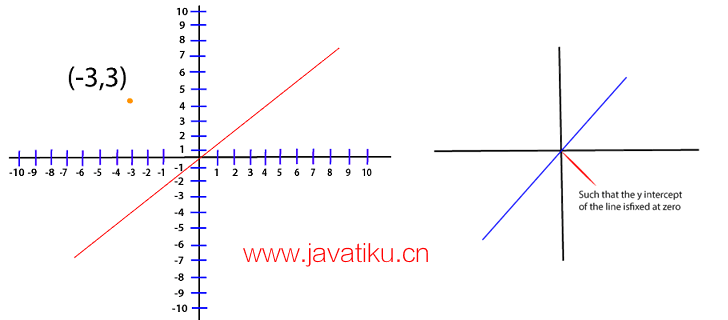

现在，无论我们处理的是哪条线，最优的线将会有一个权重，将这个误差尽可能减小到接近零。现在，我们处理的点是 (-3, 3)，对于这个损失，函数将转化为：

Loss=(3-A(-3))2
Loss=(3+3A)2

现在，我们创建一个表格，并尝试不同的 A 值，看看哪一个给我们最小的误差。

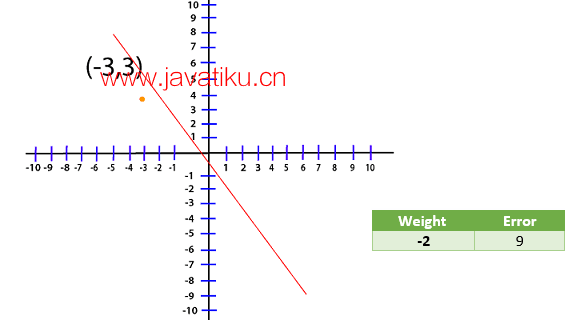
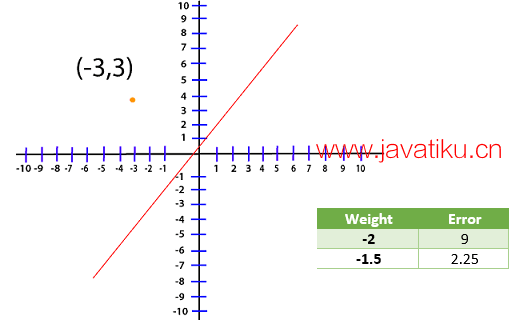
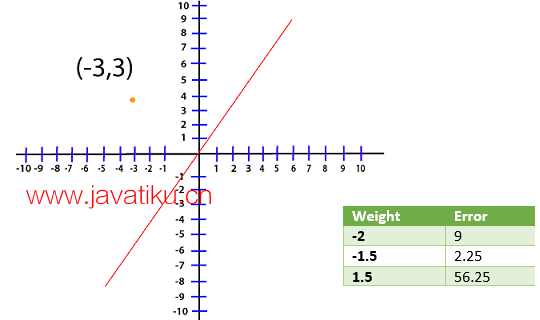
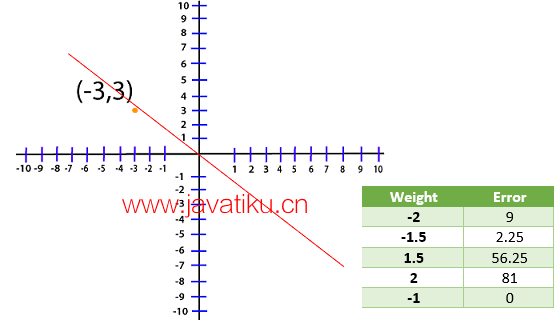
为了可视化的目的，我们在我的图水平上为不同的权重绘制了不同的误差值。

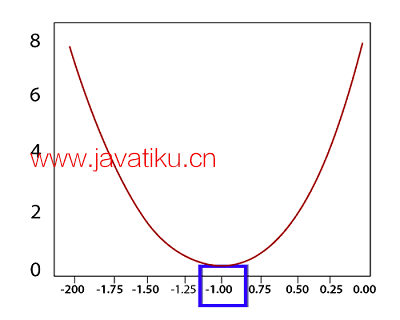
我们在我的图表层面上为了可视化目的绘制了不同权重的不同误差值。

为了训练模型知道这里的权重，我们使用梯度下降。