Python教程-Kadane算法在Python中的应用

在下面，我们将讨论Kadane算法及其用于解决“最大子数组和”问题的性质。我们将了解算法的概念，以及Python代码的示例和相应的输出。最后，我们将讨论Kadane算法的时间复杂度和Kadane算法在现实生活中的应用。

因此，让我们开始吧。

理解Kadane算法

Kadane算法是用于解决问题的流行方法之一，它借助动态规划来解决问题。正如我们已经知道，最大子数组问题被认为是动态规划领域中的热门问题之一。我们可能认为这个问题似乎很简单，问题的输出将是数组中所有数据元素的和。然而，这并不正确。我们还会在数组的数据元素中遇到负整数，它们会减小整个数组的总和。因此，我们将借助Kadane算法来解决这个问题。

Kadane算法用于查找一维整数数组中具有最大可能总和的连续子数组。在理解问题的陈述之后，每个人的主要方法将是应用蛮力方法来解决问题。然而，这样做会使解决方案的时间复杂度为O(n^2)，这并不令人印象深刻。因此，我们将使用Kadane算法来解决该问题，通过使用两个变量来跟踪到目前为止的总和和最大总和来遍历整个数组。在使用此算法时需要注意的最重要的方面是用于更新这两个变量的条件。

理解最大子数组和的算法

现在，让我们考虑最大子数组和算法的基本步骤，如下所示：

步骤1： 我们必须初始化max_till_now = 0

步骤2： 我们必须初始化max_ending = 0

步骤3： 我们必须为数组中的每个数据元素重复步骤4到步骤6。

步骤4： 我们必须设置max_ending = max_ending + a[i]

步骤5： 如果(max_ending < 0)，那么我们必须设置max_ending = 0

步骤6： 如果(max_till_now < max_ending)，那么我们必须设置max_till_now = max_ending

步骤7： 我们必须返回max_till_now

在上述算法的步骤中，我们使用max_ending 寻找数组的所有正数据元素，使用max_till_now 寻找所有正段中数据元素的最大和。因此，每当我们通过与max_till_now 进行比较获得正和时，我们将能够使用更大的和更新它。

因此，每当max_ending 变为负数时，我们将其设置为零，并在每次迭代时检查max_till_now 是否小于max_ending 的条件，以在条件返回True时更新max_till_now。

使用图示表示理解Kadane算法

让我们考虑一个整数数组的以下示例。

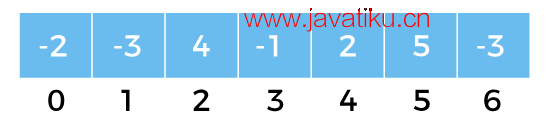
图1： 整数数组

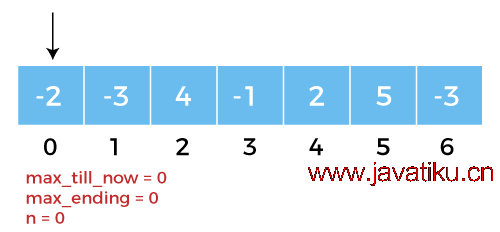
图2： 我们将初始化max_till_now = 0 和 max_ending = 0（n = 0）。

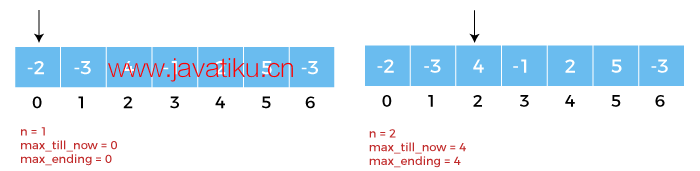
图3： 对于n = 1，我们将得到max_till_now = 0 和max_ending = 0；但是对于n = 2，我们将得到max_till_now = 4 和max_ending = 4。

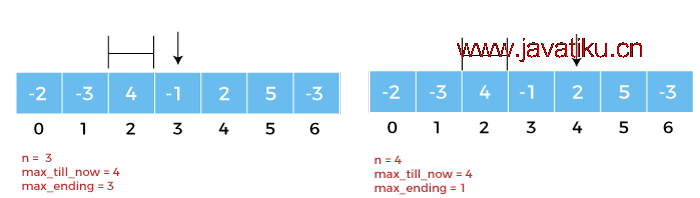
图4： 我们将分别分配值n = 3 和 4，并得到max_till_now = 4 和max_ending = 3，和max_till_now = 4 和max_ending = 1。

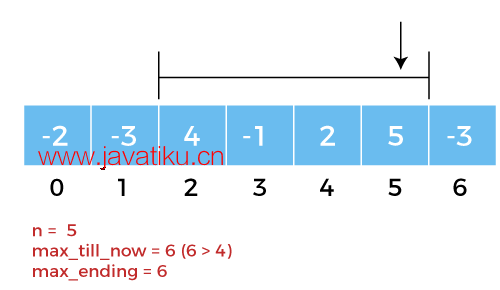
图5： 对于n = 5，我们将得到max_till_now = 6（6 > 4） 和max_ending = 6。

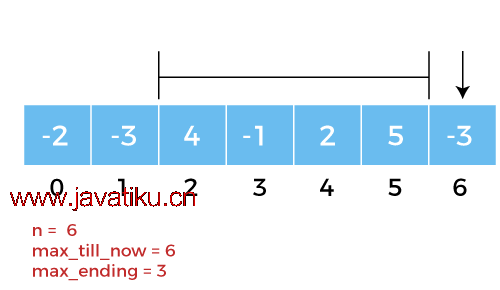
图6： 对于n = 6，我们还将得到max_till_now = 6 和max_ending = 4。

因此，从上面的示例中，我们将找到从n = 2 到n = 5 的最大子数组，最大总和为6。

使用Python代码理解Kadane算法

让我们考虑以下代码片段，演示了Kadane算法的工作方式。

示例：

# defining the function to find the maximum subarray sum  
def max_Subarray_Sum(my_array, array_size):  
    # assigning the variables  
    maxTillNow = my_array[0]  
    maxEnding = 0  
      
    # using the for-loop  
    for n in range(0, array_size):  
        maxEnding = maxEnding + my_array[n]  
        # using the if-elif-else statement  
        if maxEnding < 0:  
            maxEnding = 0  
          
        elif (maxTillNow < maxEnding):  
            maxTillNow = maxEnding  
              
    return maxTillNow  
# defining the array  
my_array = [-2, -3, 4, -1, -2, 5, -3]  
# printing the maximum subarray sum for the users  
print("Maximum Subarray Sum:", max_Subarray_Sum(my_array, len(my_array)))

输出：

Maximum Subarray Sum: 6

解释：

在上面的代码片段中，我们定义了一个名为max_Subarray_Sum的函数，该函数接受两个参数my_array和array_sum。我们然后将变量maxTillNow分配给数组的第一个索引值，将maxEnding分配为零。然后，我们使用for循环遍历整个数组。我们还使用if-elif-else条件语句，并返回maxTillNow。最后，我们定义了数组，并为用户打印最大子数组和，在上面的示例中为6。

理解时间复杂度

对于由n个整数数据元素组成的数组，Kadane算法的时间复杂度定义为O(n)，因为只有一个for循环要在整个程序中执行。同样，该算法的辅助空间复杂度为O(1)。

了解应用程序

Kadane算法有各种应用，其中一些如下所述：

Kadane算法用于查找所提供的整数数组的最大子数组和。
它用作图像处理的算法。
它还可以用于解决问题，如“顺序旅行站”和“海岸边的旅馆”。
它还用于业务分析。

结论

最后，我们可以得出结论，解决找到最大子数组和的问题陈述似乎并不容易。然而，Kadane算法简化了解决这样一个问题，并以最小的时间复杂度获得了解决方案。这是可能的，因为Kadane算法利用了收集达到解决方案所需的信息的技术，避免了不必要的数据存储。因此，我们可以将此算法视为动态规划方法的一个简单示例，具有许多实际应用程序。