Python教程-Python中的方差分析(ANOVA)测试

以下教程基于数据分析;我们将详细讨论方差分析(ANOVA),以及如何在Python编程语言中执行它。ANOVA通常在心理学研究中广泛使用。
在以下教程中,我们将学习如何使用SciPy库进行ANOVA,以及如何在Python中进行手动评估,使用Pyyttbl和Statsmodels。
理解ANOVA测试
我们可以将方差分析测试,也称为ANOVA,视为一种用于多个组的T检验的一般化。通常,我们使用独立的T检验来比较两组之间的平均值。当我们需要比较两组以上的组之间的平均值时,就会使用ANOVA测试。
ANOVA测试检查模型中平均数是否存在差异(检查是否存在总体效应);但是,这种方法不告诉我们差异的具体位置(如果存在差异的话),我们可以通过进行事后检验来找到差异的位置。
然而,为了执行任何测试,我们首先必须定义零假设和备择假设:
- 零假设:各组之间没有显著差异。
- 备择假设:各组之间存在显著差异。
我们可以通过比较两种变异来执行ANOVA测试。第一个变异是样本均值之间的变异,另一个是在每个样本内部的变异。下面的公式描述了一元ANOVA测试统计量。
ANOVA公式的输出是F统计量(也称为F比率),它使我们能够分析多组数据集中样本之间的变异和样本内部的变异。
我们可以将一元ANOVA测试的公式表示如下:

其中,
yi - 第i组的样本均值
ni - 第i组的观察次数
y - 数据的总均值
k - 组的总数
yij - 第j组中的第i个观察
N - 总样本大小
当我们绘制ANOVA表时,可以以以下格式看到上述所有组件:
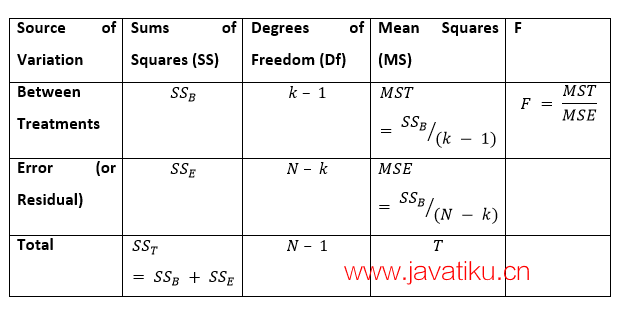
通常,如果F的p值小于0.05,则排除零假设,支持备择假设。在拒绝零假设的情况下,我们可以说所有组的均值不相等。
注意:如果在测试组之间不存在真正的差异,即零假设成立,那么ANOVA测试的F比率统计将接近1。
ANOVA测试的假设
在执行ANOVA测试之前,我们必须满足以下假设:
- 我们可以随机独立地从因子水平定义的总体中获得观察值。
- 每个因子水平的数据分布是一般的。
- 独立案例:样本案例必须相互独立。
- 方差齐性:齐性表示组之间的方差应大致相等。
我们可以使用Brown-Forsythe测试或Levene的测试来检验方差齐性的假设。我们还可以使用直方图、峰度或偏度值,以及Kolmogorov-Smirnov、Shapiro-Wilk或Q-Q图等测试来检验分数分布的正态性。我们还可以从研究设计中确定独立性的假设。
需要注意的是,如果违反了独立性假设,ANOVA测试对此不具有鲁棒性。这意味着即使有人试图违反正态性或齐性的假设,他们仍然可以执行测试并信任结果。
然而,如果违反了独立性的假设,ANOVA测试的结果将不可接受。通常,如果我们有相等大小的组,那么在违反正态性的情况下,对ANOVA测试的分析通常是可接受的,前提是样本容量足够大。
理解ANOVA测试的类型
ANOVA测试可以分为三种主要类型。这些类型如下:
- 一元ANOVA测试
- 二元ANOVA测试
- n元ANOVA测试
一元ANOVA测试
只有一个独立变量的方差分析测试称为一元ANOVA测试。
例如,一个国家可以评估冠状病毒病例的差异,一个国家可以有多个用于比较的类别。
二元ANOVA测试
有两个独立变量的方差分析测试称为二元ANOVA测试。这个测试也称为因子方差分析测试。
例如,在上面的例子中,双重ANOVA可以检查冠状病毒病例(因变量)在年龄组(第一个独立变量)和性别(第二个独立变量)之间的差异。双重ANOVA可以用于检查这两个独立变量之间的交互作用。交互作用表示差异在独立变量的所有类别之间不均匀分布。
假设老年组的冠状病毒病例总体高于年轻组;然而,与亚洲国家相比,欧洲国家中的差异可能会有所不同。
n元ANOVA测试
如果研究人员使用两个以上的独立变量,则方差分析测试被视为n元ANOVA测试。这个测试也称为多元方差分析测试(MANOVA)。
例如,我们可以同时检查国家、年龄组、性别、族裔等多个独立变量对冠状病毒病例的差异。
ANOVA测试将为我们提供一个单一(单变量)F值,而MANOVA测试将为我们提供一个多元(多变量)F值。
了解ANOVA测试中的重复性和无重复性
通常,我们可能会听到关于ANOVA测试中的重复性和无重复性的概念。让我们了解这些是什么意思:
具有重复性的二元ANOVA测试
具有重复性的二元ANOVA测试是在两个组中执行多个任务的成员的情况下进行的。
例如,假设冠状病毒疫苗仍在研发中。医生们正在为感染了该病毒的两组患者执行两种不同的治疗。
无重复性的二元ANOVA测试
无重复性的二元ANOVA测试是在只有一个组的情况下进行的,我们对同一组进行了两次测试。
例如,假设疫苗已成功研发,研究人员正在测试一组志愿者,在疫苗接种前后观察疫苗是否有效。
了解ANOVA测试后续测试
在进行ANOVA测试时,我们试图确定组之间是否存在统计显著差异。如果存在差异,我们需要测试差异的具体位置。
因此,研究人员使用事后检验来确定哪些组之间存在差异。
我们可以执行一些检验,检查各组之间的均值差异。我们可以进行多个比较检验来控制I型错误率,包括Bonferroni、Dunnet、Scheffe和Turkey检验等。
现在,我们将只了解使用Python编程语言执行一元ANOVA测试。
在Python中理解一元ANOVA测试
我们将执行执行ANOVA测试的过程分为不同的部分。
导入所需的库
为了开始使用ANOVA测试,让我们导入一些必要的库和模块。
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.formula.api import ols
import seaborn as sns
import numpy as np
import pandas.tseries
plt.style.use('fivethirtyeight') 假设
让我们为问题考虑一个假设:
"对于每种饮食,人们的体重平均值是相同的。"
加载数据
在以下问题中,我们将使用由谢菲尔德大学设计的饮食数据集。该数据集包含一个二进制变量作为性别,其中1表示男性,0表示女性。
mydata = pd.read_csv('Diet_Dataset.csv') 了解数据集
一旦我们成功导入数据集,让我们打印一些数据以了解它。
print(mydata.head()) 输出:
Person gender Age Height pre.weight Diet weight6weeks
0 25 41 171 60 2 60.0
1 26 32 174 103 2 103.0
2 1 0 22 159 58 1 54.2
3 2 0 46 192 60 1 54.0
4 3 0 55 170 64 1 63.3现在让我们打印数据集中的总行数。
print('The total number of rows in the dataset:', mydata.size) 输出:
The total number of rows in the dataset: 546检查缺失值
现在,我们必须查看数据集中是否存在缺失值。我们可以使用以下语法来检查。
print(mydata.gender.unique())
# displaying the person(s) having missing value in gender column
print(mydata[mydata.gender == ' ']) 输出:
[' ' '0' '1']
Person gender Age Height pre.weight Diet weight6weeks
0 25 41 171 60 2 60.0
1 26 32 174 103 2 103.0我们可以观察到两个条目在'gender'列中包含缺失值。现在让我们找到数据集中缺失值的总百分比。
print('Percentage of missing values in the dataset: {:.2f}%'.format(mydata[mydata.gender == ' '].size / mydata.size * 100)) 输出:
Percentage of missing values in the dataset: 2.56%正如我们所看到的,数据集中有大约3%的缺失值。我们可以选择忽略、删除或根据最接近的身高均值对其性别进行分类。
了解体重分布
在接下来的步骤中,我们将使用distplot()函数绘制图形,以了解样本数据中的体重分布。让我们考虑以下代码片段。
f, ax = plt.subplots( figsize = (11,9) )
plt.title( 'Weight Distributions among Sample' )
plt.ylabel( 'pdf' )
sns.distplot( mydata.weight6weeks )
plt.show() 输出:
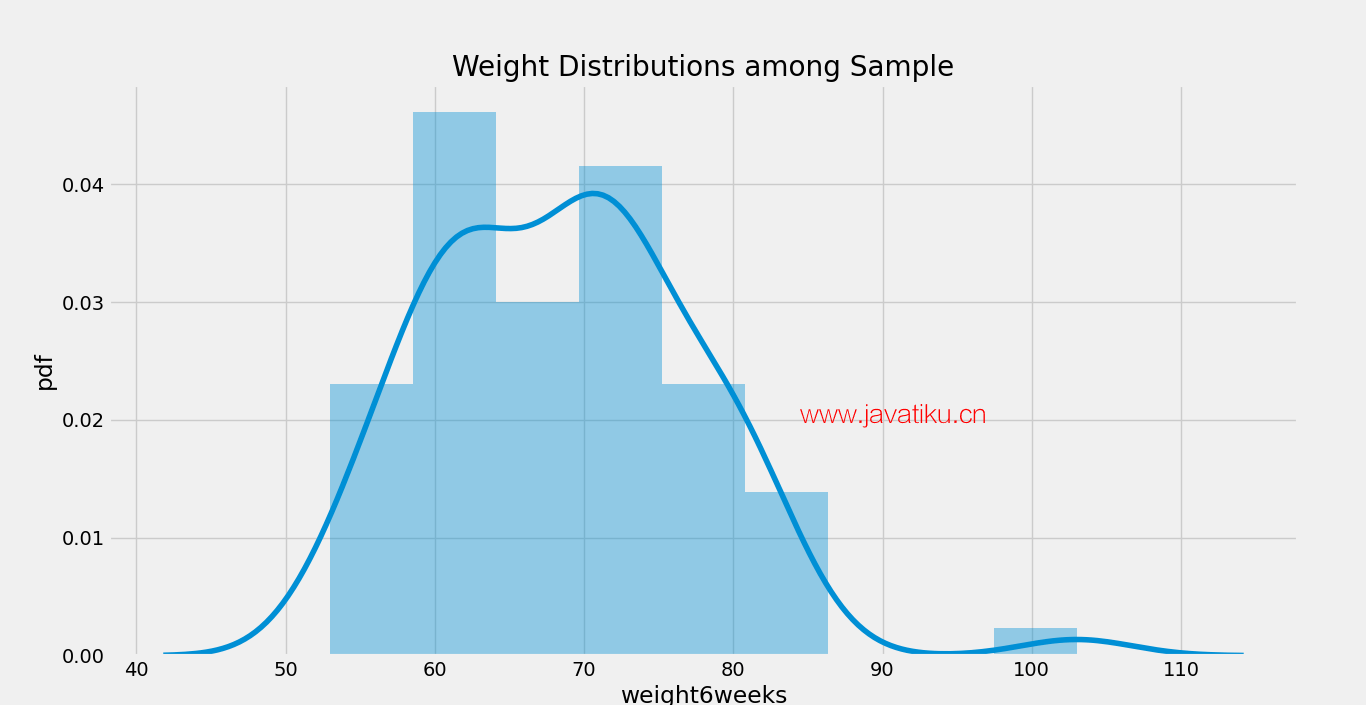
我们还可以为数据集中的每个性别绘制分布图。以下是该操作的语法。
f, ax = plt.subplots( figsize = (11,9) )
sns.distplot( mydata[mydata.gender == '1'].weight6weeks, ax = ax, label = 'Male')
sns.distplot( mydata[mydata.gender == '0'].weight6weeks, ax = ax, label = 'Female')
plt.title( 'Weight Distribution for Each Gender' )
plt.legend()
plt.show() 输出:
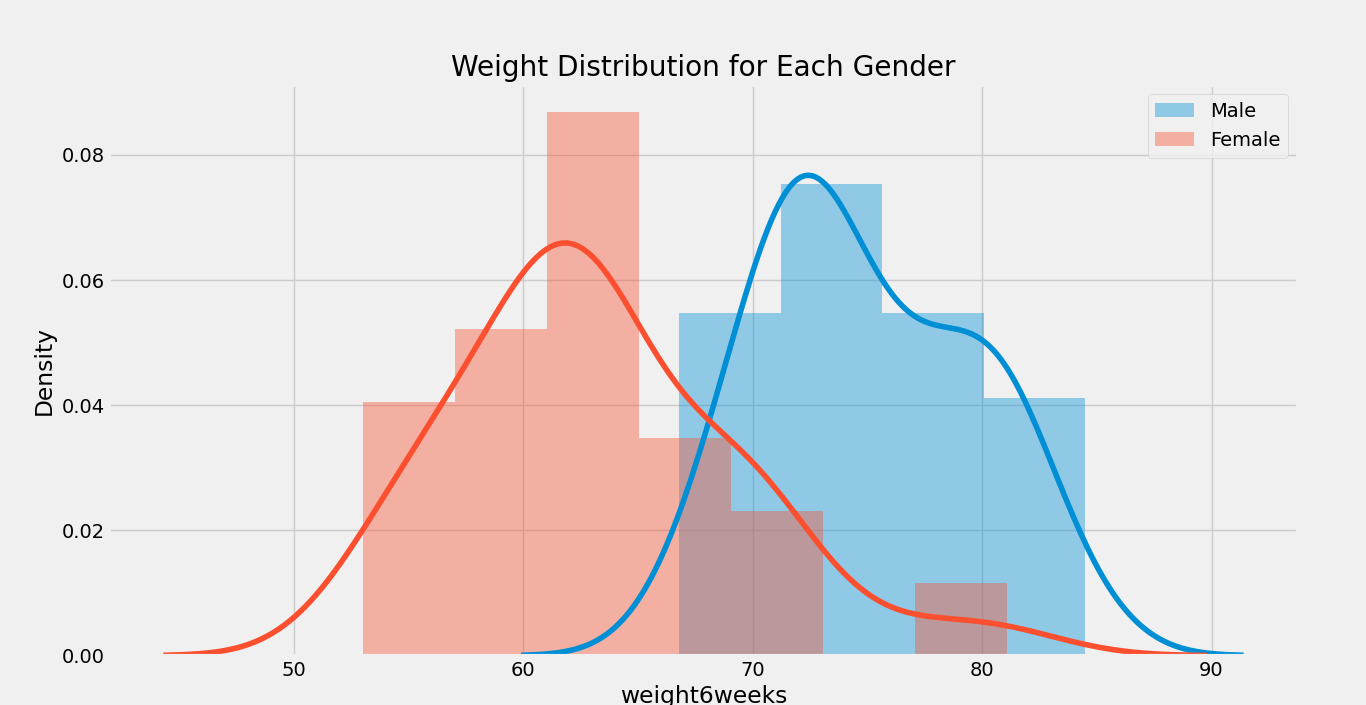
我们还可以使用以下函数来显示每个性别的分布图。
def infergender(x):
if x == '1':
return 'Male'
if x == '0':
return 'Female'
return 'Other'
def showdistribution(df, gender, column, group):
f, ax = plt.subplots( figsize = (11, 9) )
plt.title( 'Weight Distribution for {} on each {}'.format(gender, column) )
for groupmember in group:
sns.distplot(df[df[column] == groupmember].weight6weeks, label='{}'.format(groupmember))
plt.legend()
plt.show()
uniquediet = mydata.Diet.unique()
uniquegender = mydata.gender.unique()
for gender in uniquegender:
if gender != ' ':
showdistribution(mydata[mydata.gender == gender], infergender(gender), 'Diet', uniquediet) 输出:
图1:
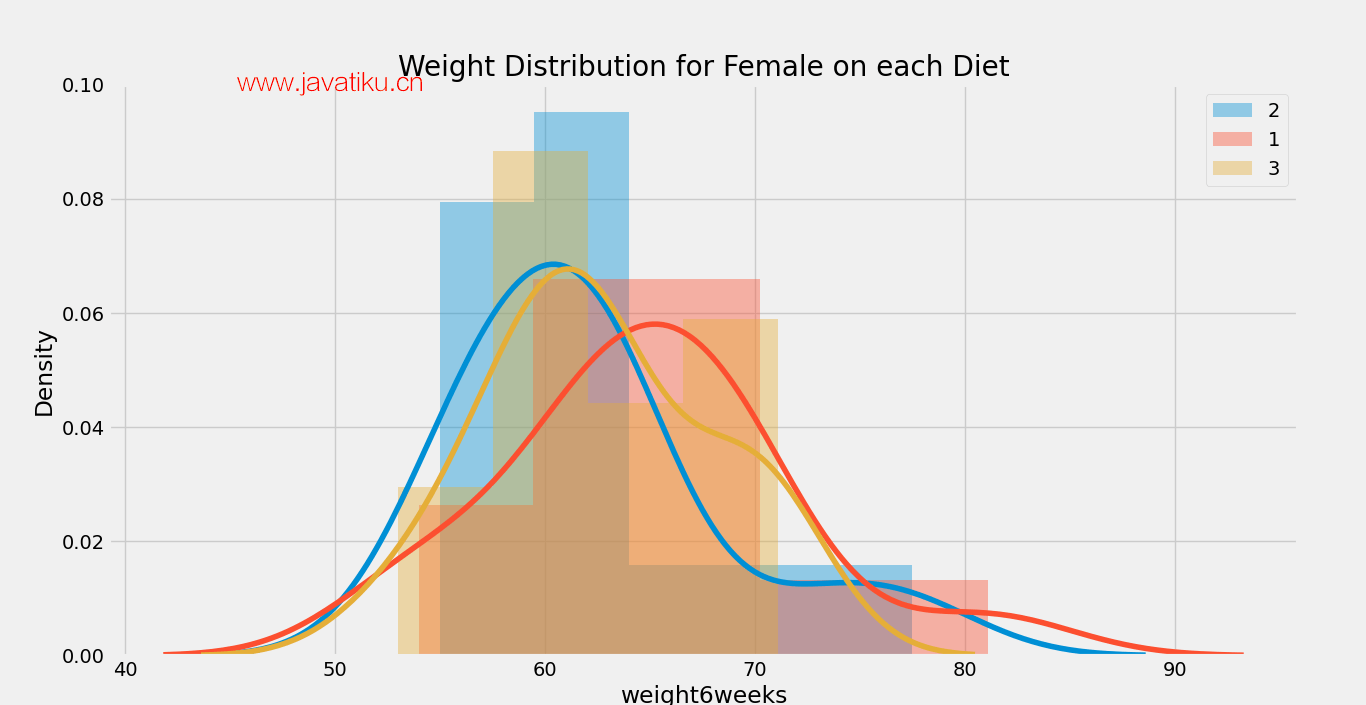
图2:
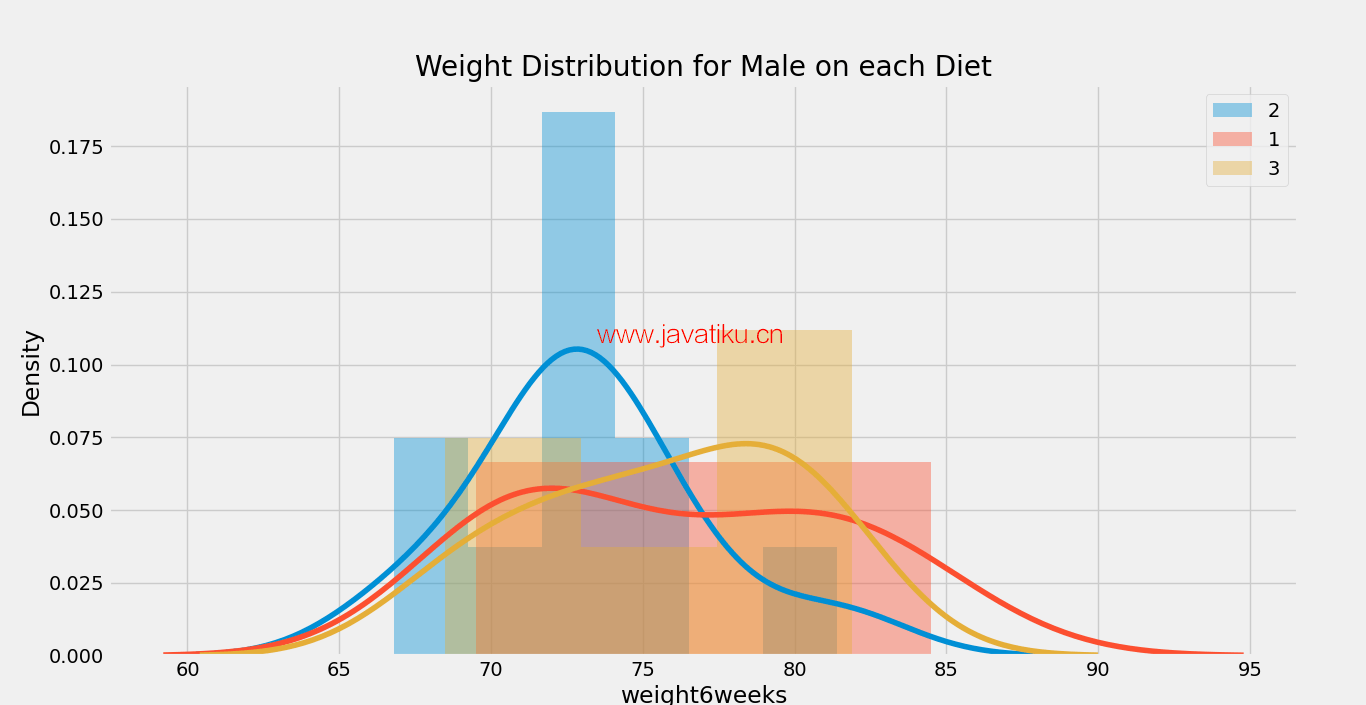
现在,我们将根据'gender'列计算均值、中位数、非零计数和标准差。
print(mydata.groupby('gender').agg(
[ np.mean, np.median, np.count_nonzero, np.std ]
).weight6weeks) 输出:
mean median count_nonzero std
gender
81.500000 81.5 2.0 30.405592
0 63.223256 62.4 43.0 6.150874
1 75.015152 73.9 33.0 4.629398正如我们所看到的,我们已经根据性别估计了所需的统计测量。我们还可以根据性别和饮食将这些统计测量分类。
print(mydata.groupby(['gender', 'Diet']).agg(
[np.mean, np.median, np.count_nonzero, np.std]
).weight6weeks) 输出:
mean median count_nonzero std
gender Diet
2 81.500000 81.50 2.0 30.405592
0 1 64.878571 64.50 14.0 6.877296
2 62.178571 61.15 14.0 6.274635
3 62.653333 61.80 15.0 5.370537
1 1 76.150000 75.75 10.0 5.439414
2 73.163636 72.70 11.0 3.818448
3 75.766667 76.35 12.0 4.434848我们可以观察到饮食对女性体重有轻微的影响,但似乎不会影响男性。
执行一元ANOVA测试
一元ANOVA测试的零假设是:

这个测试尝试检查这个假设是否成立。
让我们首先确定置信水平为95%,这意味着我们将仅接受5%的错误率。
mymod = ols('Height ~ Diet', data = mydata[mydata.gender == '0']).fit()
# performing type 2 anova test
aovtable = sm.stats.anova_lm(mymod, typ = 2)
print('ANOVA table for Female')
print('----------------------')
print(aovtable)
print()
mod = ols('Height ~ Diet', data = mydata[mydata.gender=='1']).fit()
# performing type 2 anova test
aovtable = sm.stats.anova_lm(mymod, typ = 2)
print('ANOVA table for Male')
print('----------------------')
print(aovtable) 输出:
ANOVA table for Female
----------------------
sum_sq df F PR(>F)
Diet 559.680764 1.0 7.17969 0.010566
Residual 3196.086677 41.0 NaN NaN
ANOVA table for Male
----------------------
sum_sq df F PR(>F)
Diet 559.680764 1.0 7.17969 0.010566
Residual 3196.086677 41.0 NaN NaN在上面的输出中,我们可以观察到男性和女性的两个p值(PR(>F))。
对于男性,我们无法在95%置信水平以下接受以下零假设,因为p值大于alpha值,即0.05 < 0.512784。因此,在提供这三种类型的饮食后,我们没有发现男性体重方面的差异。
对于女性,由于p值PR(>F)低于错误率,即0.05 > 0.010566,我们可以拒绝零假设。这意味着我们非常有信心地认为女性在饮食方面的身高存在差异。
因此,现在我们了解了饮食对女性的影响,但我们不知道饮食对男性的影响。
因此,在接下来的步骤中,让我们进行多重比较检验。我们将使用Scheffe方法,该方法提供了一个合适的校正,使我们可以在所有饮食之间进行比较,同时避免I型错误。
from statsmodels.stats.multicomp import pairwise_tukeyhsd, MultiComparison
# using the female data only
mydf = mydata[mydata.gender == '0']
# comparing the height between each diet, using 95% confidence interval
multiComp = MultiComparison(mydf['Height'], mydf['Diet'])
tukeyres = multiComp.tukeyhsd(alpha = 0.05)
print(tukeyres)
print('Unique diet groups: ', multiComp.groupsunique) 输出:
Multiple Comparison of Means - Tukey HSD, FWER=0.05
=====================================================
group1 group2 meandiff p-adj lower upper reject
-----------------------------------------------------
1 2 -3.5714 0.5437 -11.7861 4.6432 False
1 3 -8.7714 0.0307 -16.848 -0.6948 True
2 3 -5.2 0.2719 -13.2766 2.8766 False
-----------------------------------------------------
Unique diet groups: [1 2 3]根据上述输出可以观察到,我们只能在第1和第3种饮食类型中拒绝零假设,这意味着在饮食1和饮食3的体重方面存在统计显著差异。



