Python教程-Python中的曲线拟合

介绍
曲线拟合是一种优化方法,它寻找适合给定一组观测值的定义函数的最佳参数集。
与监督学习不同,曲线拟合需要我们定义将输入示例映射到输出的函数。用于映射的函数也称为基础函数,它可以是我们喜欢的任何形式,如直线(线性回归)、曲线(多项式回归)等。这个映射函数提供了灵活性和控制,以定义曲线的形状,优化过程用于找到函数的特定最佳参数。
在以下教程中,我们将了解什么是曲线拟合以及如何在Python中执行它。
在教程结束时,我们将了解以下内容:
- 曲线拟合涉及查找函数的最佳参数,将输入示例映射到输出。
- Python库SciPy提供了一个API,用于将曲线拟合到数据集。
- 使用SciPy中的曲线拟合将不同类型的曲线拟合到观测集。
理解曲线拟合
正如前面所讨论的,曲线拟合是一个优化问题,它允许我们找到适合一组观测值的线。
当我们将二维空间中的曲线拟合看作是图表时,它变得更容易理解。
假设我们从问题领域收集了包括输入和输出的示例数据。
图表的x轴充当独立变量,即函数的输入。另一方面,图表的y轴充当依赖变量,即函数的输出。我们可能不知道将输入示例映射到输出的函数形式,但我们可以使用标准函数形式来近似函数。
曲线拟合包括以下阶段:
- 首先,定义映射函数的函数形式(也称为目标函数或基础函数)。
- 然后,搜索函数的参数,以产生最小误差的参数。
误差是使用问题领域提供的观测值估计的,方法是将输入传递给候选目标函数并估计输出。计算得到的输出与实验输出进行比较。
一旦我们完成了拟合,就可以使用基础函数来插值或外推域中的新点。通常使用基础函数对一系列输入值执行值,并根据结果绘制线图,显示输入和输出之间的差异,并拟合到观察点。
曲线拟合的解释在于基础函数的形式。直线可以使用以下公式描述:
y = a × x + b
其中y是估计的输出,x是输入,a和b是通过优化算法找到的基础函数的参数。
这个方程被称为线性方程,因为它是输入的加权和。
在线性回归模型中,这些参数被称为系数,而在神经网络中,这些参数被称为权重。
我们可以将这个方程推广到任意数量的输入,这意味着曲线拟合的概念不仅限于两个维度(一个是输入,另一个是输出)。它可以包含多个输入变量。
例如,具有两个输入变量的线性方程的公式可能如下所示:
y = a1 × x1 + a2 × x2 + b
方程不一定是一条直线。
我们可以通过插入指数来向目标函数添加曲线。例如,我们可以插入另一个参数加权的输入的平方版本,如下所示:
y = a × x + b × x2 + c
这个方程被称为多项式回归,而平方项指的是二次多项式。
可以通过最小二乘法对这种类型的线性方程进行拟合并进行解析估计,这意味着我们可以使用一些线性代数找到参数的最佳值。
有些人可能还想在方程中包含其他数学函数,如sin、cos、tan等。每个项都使用参数加权,并添加到整个方程以生成输出:
y = a × sin(b × x) + c
通过将任意数学函数添加到目标函数中,我们不能通过解析方法估计参数,而需要使用迭代优化算法。
这个方程被称为非线性最小二乘法,因为映射函数不再是凸的(它是非线性的),不太容易求解。
现在,我们已经成功理解了曲线拟合的概念,是时候继续了解如何在Python中执行曲线拟合了。
在Python中执行曲线拟合
可以使用Python为数据集执行曲线拟合。Python提供了一个名为SciPy的开源库。这个SciPy库包含一个名为curve_fit()的函数,用于通过非线性最小二乘法进行曲线拟合。
curve_fit()函数以与输出数据相同的输入和输出数据作为参数,还包括要使用的目标函数的名称。
目标函数必须包括输入数据的示例以及一些参数数量。剩下的参数将成为优化过程将优化的系数或权重常数。
让我们考虑一个演示示例,以理解这个概念。
假设我们有一些来自领域的观测值作为x个输入变量和y个输出变量。
语法:
...
# loading the input variables from a file
values_x = ...
values_y = ... 现在,我们需要设计一个目标函数,以适应数据,并将其实现为Python中的函数,该函数接受输入以及参数。
让我们假设这个函数是一条直线,如下所示:
语法:
# defining a mapping function
def mapping(x, a, b, c):
return a * x + b 一旦定义了函数,我们可以调用curve_fit()函数,以使用定义的映射函数将一条直线拟合到数据集中。
curve_fit()函数将返回目标函数的最佳值,例如系数的值。该函数还将返回用于计算参数的协方差矩阵,但可以暂时忽略它。
语法:
...
# calling a the curve_fit() function
popt, _ = curve_fit(mapping, values_x, values_y) 拟合成功后,我们可以使用最佳参数和目标函数mapping()来评估任何主观输入的输出。
该函数可能包含来自领域已经收集的示例的输出。它可能包含一些新的值,可以插入到观察到的值中。它还可能包括超出观察值范围的外推值。
语法:
...
# defining new input values
new_x = ...
# unpacking the optimal arguments for the mapping function
a, b, c = popt
# using the optimal arguments to estimate new values
new_y = mapping(new_x, a, b, c) 由于我们已经了解了如何使用曲线拟合的API,让我们看一个工作示例。
Python中曲线拟合的工作示例
让我们从导入项目所需的包和库开始。
语法:
# importing the required packages and libraries
from scipy.optimize import curve_fit
from numpy import array, exp
import matplotlib.pyplot as plt 导入包后,我们需要测试数据来执行曲线拟合。因此,我们将定义基本输入数据x和输出数据y如下。
语法:
# defining the variables
values_y = array([11, 10, 12, 14, 15, 15, 14, 13, 14, 11, 10, 11, 7, 9, 8, 6, 5])
values_x = array(range(len(values_y))) 然后,我们将定义一些映射函数,以便使用curve_fit()方法并验证它们在拟合中的差异。我们将使用以下方程式作为映射函数:
1.y = ax2 + bx + c
2.y = ax3 + bx + c
3.y = ax3 + bx2 + c
4.y = a × exp?(bx) + c
该过程如下语法所示:
语法:
# defining objective functions
def mapping1(values_x, a, b, c):
return a * values_x**2 + b * values_x + c
def mapping2(values_x, a, b, c):
return a * values_x**3 + b * values_x + c
def mapping3(values_x, a, b, c):
return a * values_x**3 + b * values_x**2 + c
def mapping4(values_x, a, b, c):
return a * exp(b * values_x) + c 通过curve_fit()函数使用这些方程拟合数据非常简单,该函数提供了映射函数、数据x和y。curve_fit()方法将返回目标函数的最佳参数。例如,系数的值。该函数还将返回计算参数的协方差矩阵的输出。
语法:
# using the curve_fit() function
args, covar = curve_fit(mapping1, values_x, values_y)
print("Arguments: ", args)
print("Co-Variance: ", covar) 输出:
Arguments: [-0.08139835 0.8636481 11.1362229 ]
Co-Variance: [[ 2.38376125e-04 -3.81401800e-03 9.53504499e-03]
[-3.81401800e-03 6.55534344e-02 -1.88793892e-01]
[ 9.53504499e-03 -1.88793892e-01 7.79966692e-01]]正如我们所看到的,curve_fit()函数计算出了目标函数的最佳参数和协方差。我们随后打印了这些值供用户查看。
我们将通过配置目标函数和数据x和y到curve_fit()方法来开始拟合数据,然后获取包含a、b和c值的结果数据。由于这里我们不使用协方差的值,所以可以跳过它。然后,我们将使用为每个函数派生的a、b和c值估算y值。
语法:
args, _ = curve_fit(mapping1, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit1 = a * values_x**2 + b * values_x + c
args, _ = curve_fit(mapping2, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit2 = a * values_x**3 + b * values_x + c
args, _ = curve_fit(mapping3, values_x, values_y)
a, b, c = args[0], args[1], args[2]
y_fit3 = a * values_x**3 + b * values_x**2 + c
args, _ = curve_fit(mapping4, values_x, values_y)
a, b, c = args[0], args[1], args[2]
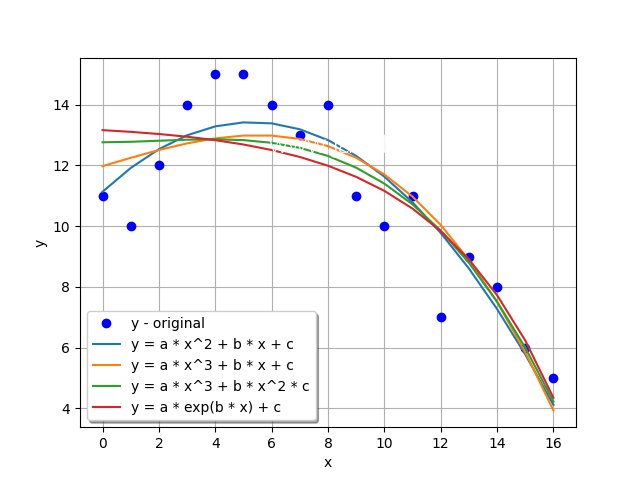
y_fit4 = a * exp(values_x * b) + c 最后,我们将绘制图表以在视觉上验证差异。以下是该语法:
语法:
# plotting the graph
plt.plot(values_x, values_y, 'bo', label="y - original")
plt.plot(values_x, y_fit1, label="y = a * x^2 + b * x + c")
plt.plot(values_x, y_fit2, label="y = a * x^3 + b * x + c")
plt.plot(values_x, y_fit3, label="y = a * x^3 + b * x^2 * c")
plt.plot(values_x, y_fit4, label="y = a * exp(b * x) + c")
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc = 'best', fancybox = True, shadow = True)
plt.grid(True)
plt.show()程序的结果图如下所示:
图表: