Python教程-Python中的T检验

简介

众所周知，Python提供了各种统计库，其中一些非常流行，比如PyMC3和SciPy。这些库为用户提供了不同的预定义函数，以便计算各种测试。但为了理解背后的数学原理，了解后台发生了什么是至关重要的。在以下教程中，我们将了解如何使用NumPy在Python中执行T检验。

T检验是统计学中最常用的程序之一。然而，即使经常使用T检验的许多人也不清楚他们的数据在背景中被处理时会发生什么，使用诸如R和Python等应用程序。

但在开始之前，让我们了解一下T检验是什么。

理解T检验

T检验是一种比较两个平均值（也称为均值）的测试，它告诉我们它们是否相互不同。T检验也被称为学生T检验，它还告诉我们这些差异有多显著。换句话说，它为我们提供了这些差异是否可能是偶然发生的信息。

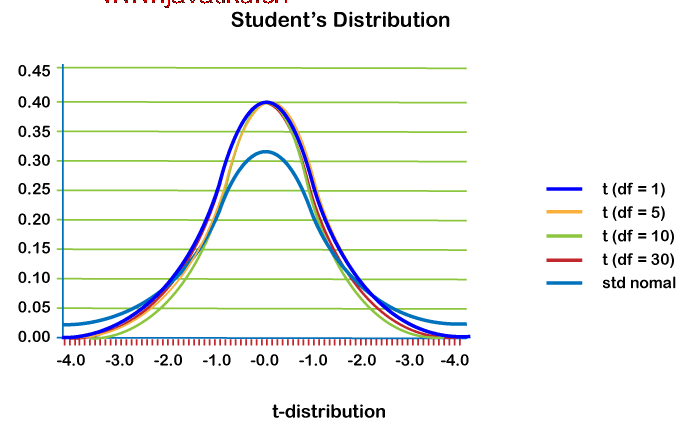
现在，让我们理解一些例子。

假设我们发烧了，尝试了一种自然疗法。发烧持续了几天。下一次发烧时，我们去药店买了一种非处方药。这次发烧持续了一周。当我们调查我们的朋友时，我们发现，当他们服用了顺势疗法药物时，他们的发烧时间更短（平均为3天）。在这项调查中，我们需要知道的是，这些结果是否可重复？T检验将通过比较这两组的平均值以及这些结果可能是偶然发生的概率来告诉我们。

在现实生活中，我们也可以使用学生T检验来比较均值。例如，一家药物公司想要测试一种新的抗癌药物，以检查它对寿命的改善。在实验中，通常会有一个对照组（提供“糖丸”或安慰剂的组）。对照组的平均预期寿命可能超过五年，而服用新药物的组可能平均预期寿命超过六年。因此，我们可以说药物可能有效，但也有可能是因为偶然事件。因此，研究人员将使用学生T检验来找出这些结果是否对整个人群可重复。

现在，让我们了解一下T值是什么。

理解T值

T值是两组之间的差异与组内差异之间的比率。如果T值更大，这意味着组之间存在更大的差异。与此同时，较小的T值表示组之间的相似性更大。T值为三（3）表示两组之间相差三倍，以及在各自组内。当我们在进行T检验时得到更大的T值时，结果更有可能是可重复的。

因此，我们可以得出以下结论：

大T值意味着组之间存在差异。
小T值意味着组之间相似。

现在，让我们了解一下T值和P值。

理解T值和P值

每个T值都包含一个P值。P值表示样本数据的结果是偶然发生的概率。P值的取值范围从0%到100%。它们通常以小数形式表示。例如，10%的P值是0.1。低P值通常是好的。较低的P值表示数据不是偶然发生的。例如，0.1的P值表示实验结果仅有1%的可能性是偶然发生的。通常，在许多情况下，接受0.05，即5%的P值，意味着数据被认为是有效的。

现在，让我们了解T检验的类型。

T检验的类型有哪些？

T检验有三种重要的类型：

独立样本T检验： 用于比较两组的平均值或均值。
配对样本T检验： 用于比较同一组在不同时间的均值（例如，相隔一年）。
单样本T检验： 用于测试单一组的均值是否与已知均值相同。

现在，让我们开始执行一个样本T检验。

执行样本T检验

假设我们需要测试人群中男性的身高是否与女性的身高有所不同。因此，我们将从人群中抽取一个样本，并使用T检验来检查结果是否显著。

我们将按照以下步骤进行：

步骤1： 确定零假设和备择假设

步骤2： 收集样本数据

步骤3： 确定置信区间和自由度

步骤4： 计算T统计量

步骤5： 从T分布中计算关键T值

步骤6： 将关键T值与计算的T统计量进行比较

让我们简要了解上述步骤。

确定零假设和备择假设

首先，定义零假设和备择假设是必要的。通常，零假设会表明两个被测试的人群在统计上没有显著差异。另一方面，备择假设将表明存在差异。对于此示例，我们可以得出以下结论：

零假设： 男女身高相同。
备择假设： 男性身高与女性身高不同。

收集样本数据

确定假设后，我们将开始从每个人群组收集数据。对于此示例，我们将收集两组数据。一个数据集包含男性的身高，另一个包含女性的身高。样本数据的大小理想情况下应相同，但可以不同。假设样本数据的大小分别为nx和ny。

确定置信区间和自由度

置信区间通常称为alpha（α）。 alpha（α）的典型值为0.05。这意味着有95%的置信度可以对测试的结论进行验证。我们可以使用以下公式定义自由度：

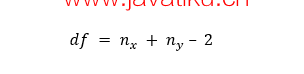
计算T统计量

我们可以使用以下公式来计算t统计量：

M = 均值

n = 每组的分数数

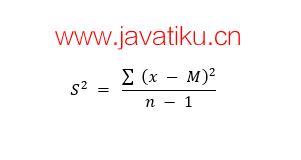
x = 个体分数

M = 均值

n = 组内的分数数

此外，Mx和My是两个女性和男性样本的均值的值。 Nx和Ny是两个样本的样本空间，S是标准差。

从T分布中计算关键T值

我们需要两个对象来计算关键t值。第一个是alpha的选择值，另一个是自由度。关键t值的计算公式复杂，但对于固定的自由度对和alpha的值来说是固定的。因此，我们使用表来计算关键t值。

然而，Python在SciPy库中提供了一个函数，可以完成相同的任务。

将关键T值与计算的T统计量进行比较

一旦计算出关键T值，我们将该值与之前计算的T统计量进行比较。如果关键t值小于计算的T统计量，则测试推断出两个人群在统计上存在显著差异。因此，我们必须拒绝零假设，即两个样本在统计上没有显著差异。

但在另一种情况下，两个人群之间没有显著差异，测试未能拒绝零假设。因此，我们接受备择假设，即男性和女性的身高在统计上有显著差异。

让我们考虑以下Python程序，演示了该模型的工作原理。

程序:

# Importing the required libraries and packages  
import numpy as np  
from scipy import stats  
# Defining two random distributions  
# Sample Size  
N = 10  
# Gaussian distributed data with mean = 2 and var = 1  
x = np.random.randn(N) + 2  
# Gaussian distributed data with mean = 0 and var = 1  
y = np.random.randn(N)  
# Calculating the Standard Deviation  
# Calculating the variance to get the standard deviation  
var_x = x.var(ddof = 1)  
var_y = y.var(ddof = 1)  
# Standard Deviation  
SD = np.sqrt((var_x + var_y) / 2)  
print("Standard Deviation =", SD)  
# Calculating the T-Statistics  
tval = (x.mean() - y.mean()) / (SD * np.sqrt(2 / N))  
# Comparing with the critical T-Value  
# Degrees of freedom  
dof = 2 * N - 2  
# p-value after comparison with the T-Statistics  
pval = 1 - stats.t.cdf( tval, df = dof)  
print("t = " + str(tval))  
print("p = " + str(2 * pval))  
## Cross Checking using the internal function from SciPy Package  
tval2, pval2 = stats.ttest_ind(x, y)  
print("t = " + str(tval2))  
print("p = " + str(pval2))

输出:

Standard Deviation = 0.7642398582227466
t = 4.87688162540348
p = 0.0001212767169695983
t = 4.876881625403479
p = 0.00012127671696957205

说明:

在上面的示例中，我们导入了所需的库并定义了包含数据样本大小的变量。然后，我们计算了高斯分布数据和标准差。之后，我们计算了T统计量并将其与关键T值进行比较。为此，我们计算了自由度并比较了P值。一旦进行了比较，我们将值打印出来供用户参考。最后，我们使用SciPy包的函数再次比较了这些值并将它们打印出来。