Python教程-在Python中使用ARIMA模型

介绍时间序列预测
一系列在恒定时间间隔内记录指标的序列被称为时间序列。
根据频率,时间序列可以分为以下几类:
- 年度(例如,年度预算)
- 季度(例如,开支)
- 月度(例如,航空客流量)
- 周度(例如,销售数量)
- 每日(例如,天气)
- 每小时(例如,股票价格)
- 每分钟(例如,呼叫中心的呼入呼叫)
- 每秒(例如,Web流量)
一旦我们完成了时间序列分析,就必须进行预测,以预测系列将来的值。
但是,为什么需要预测?
因为预测时间序列,例如销售和需求,通常具有令人难以置信的商业价值,这增加了对预测的需求。
时间序列预测通常在许多制造公司中使用,因为它驱动主要的业务规划、采购和生产活动。任何预测的错误都将在供应链或任何业务框架的链条中波动。因此,为了获得准确的预测、节省成本并取得成功,这是非常重要的。
时间序列预测的概念和技术也可以应用于任何业务,包括制造业。
时间序列预测可以大致分为两类:
- 单变量时间序列预测: 单变量时间序列预测是一种时间序列的预测,其中我们仅使用时间序列的先前值来猜测未来值。
- 多变量时间序列预测: 多变量时间序列预测是一种时间序列的预测,其中我们使用除时间序列之外的预测因子,也称为外生变量,来进行预测。
在下面的教程中,我们将了解一种称为ARIMA建模的具体方法。
自回归积分移动平均模型,简称ARIMA,是一种用于预测的算法,其基本概念是只使用时间序列的先前值来预测未来值。
让我们详细了解ARIMA模型。
ARIMA模型介绍
ARIMA是“自回归积分移动平均”的缩写,是一种模型类,它根据其先前值(滞后项)和预测误差的滞后来“展示”给定时间序列,以便可以利用该方程来进行预测未来值。
我们可以使用ARIMA模型建模任何非季节性的、表现出模式的时间序列,而不是随机白噪声。
ARIMA模型有三个术语:
p、q和d
其中,
- p = AR项的阶数
- q = MA项的阶数
- d = 使时间序列平稳所需的差分次数
如果一个时间序列具有季节性模式,我们必须插入季节性周期,它就成为SARIMA,简称“季节性ARIMA”。
现在,在了解“AR项的阶数”之前,让我们讨论一下“d”项。
ARIMA模型中的“p”、“q”和“d”是什么?
第一步是使时间序列平稳,以建立ARIMA模型。这是因为ARIMA中的“自回归”一词意味着使用滞后项作为预测因子的线性回归模型。正如我们已经知道的,线性回归模型对于独立和不相关的预测因子效果良好。
为了使时间序列平稳,我们将使用最常见的方法,即从当前值中减去过去值。有时,根据时间序列的复杂性,可能需要多次减法。
因此,d的值是使时间序列平稳所需的最小减法次数。如果时间序列已经平稳,d为0。
现在,让我们了解“p”和“q”这两个术语。
“p”是“AR”(自回归)项的阶数,这意味着要使用的Y的滞后项数量。“q”是“MA”(移动平均)项的阶数,这意味着在ARIMA模型中应使用的滞后预测误差的数量。
现在,让我们详细了解“AR”和“MA”模型。
理解自回归(AR)和移动平均(MA)模型
在下面的部分中,我们将讨论AR和MA模型以及这些模型的实际数学公式。
一个纯AR(自回归)模型是一个仅依赖于自己滞后值的模型。因此,我们也可以得出结论,它是'Yt的滞后'的函数。
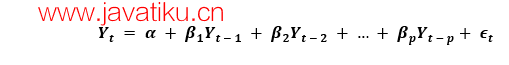
其中,Yt-1是该系列的滞后1。β1是滞后1的系数,由模型计算得出的截距项。
同样,一个纯MA(移动平均)模型是一个模型,其中Yt仅依赖于滞后的预测误差。

在这里,误差项是相应滞后的AR模型误差。误差项ϵt和ϵt-1是以下方程中的误差:
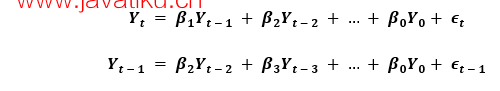
因此,我们分别得出了自回归(AR)和移动平均(MA)模型。
现在让我们理解ARIMA模型的方程。
ARIMA模型是一个模型,其中时间序列至少减去一次,以使其稳定,并结合了自回归(AR)和移动平均(MA)项。因此,我们得到以下方程:
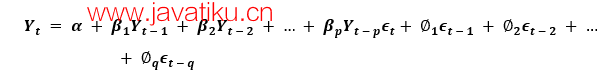
ARIMA模型的解释:
预测的Yt = 常数 + Y的滞后线性组合(最多p个滞后项)+ 滞后预测误差的线性组合(最多q个滞后项)
因此,该模型的目标是找到p、q和d的值。但是,我们如何找到它们呢?
让我们从在ARIMA模型中找到“d”开始。
在ARIMA模型中找到差分阶数'd'的方法
ARIMA模型中差分的主要目的是使时间序列稳定。
然而,我们必须注意不要过度差分序列,因为过度差分的序列也可能是稳定的,这会影响后续模型的参数。
现在,让我们理解适当的差分阶数。
最适当的差分阶数是为了实现围绕定义的均值漫游并且ACF曲线相对较快地达到零的几乎稳态系列所需的最小差分。如果自相关在多个滞后期(通常是十个或更多)上是正的,则需要进一步差分。相反,如果滞后1自相关非常负面,那么系列可能已经过度差分。
在我们无法真正决定两个差分阶数之间时,我们必须选择在差分系列中提供最小标准差的阶数。
让我们考虑一个示例来检查系列是否稳定。我们将使用Python编程语言的statsmodels包中的增广迪基-富勒测试(adfuller())。
例子:
from statsmodels.tsa.stattools import adfuller
from numpy import log
import pandas as pd
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
res = adfuller( mydata.value.dropna())
print('Augmented Dickey-Fuller Statistic: %f' % res[0])
print('p-value: %f' % res[1]) 输出:
Augmented Dickey-Fuller Statistic: -2.464240
p-value: 0.124419解释:
在上面的示例中,我们导入了adfuller模块以及numpy的log模块和pandas。然后,我们使用pandas库读取CSV文件。接着,我们使用adfuller方法并将值打印给用户。
检查系列是否稳定是必要的。如果不是,我们必须进行差分,否则d将变为零。
增广迪基-富勒(ADF)测试的零假设是时间序列不稳定。因此,如果ADF测试的p值小于显著性水平(0.05),则我们将拒绝零假设,并推断时间序列绝对稳定。正如我们可以观察到的,p值大于显著性水平。因此,我们可以对系列进行差分,并检查自相关图,如下所示。
示例:
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,7), 'figure.dpi' : 120})
# Importing data
df = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# The Genuine Series
fig, axes = plt.subplots(3, 2, sharex = True)
axes[0, 0].plot(df.value); axes[0, 0].set_title('The Genuine Series')
plot_acf(df.value, ax = axes[0, 1])
# Order of Differencing: First
axes[1, 0].plot(df.value.diff()); axes[1, 0].set_title('Order of Differencing: First')
plot_acf(df.value.diff().dropna(), ax = axes[1, 1])
# Order of Differencing: Second
axes[2, 0].plot(df.value.diff().diff()); axes[2, 0].set_title('Order of Differencing: Second')
plot_acf(df.value.diff().diff().dropna(), ax = axes[2, 1])
plt.show() 输出:
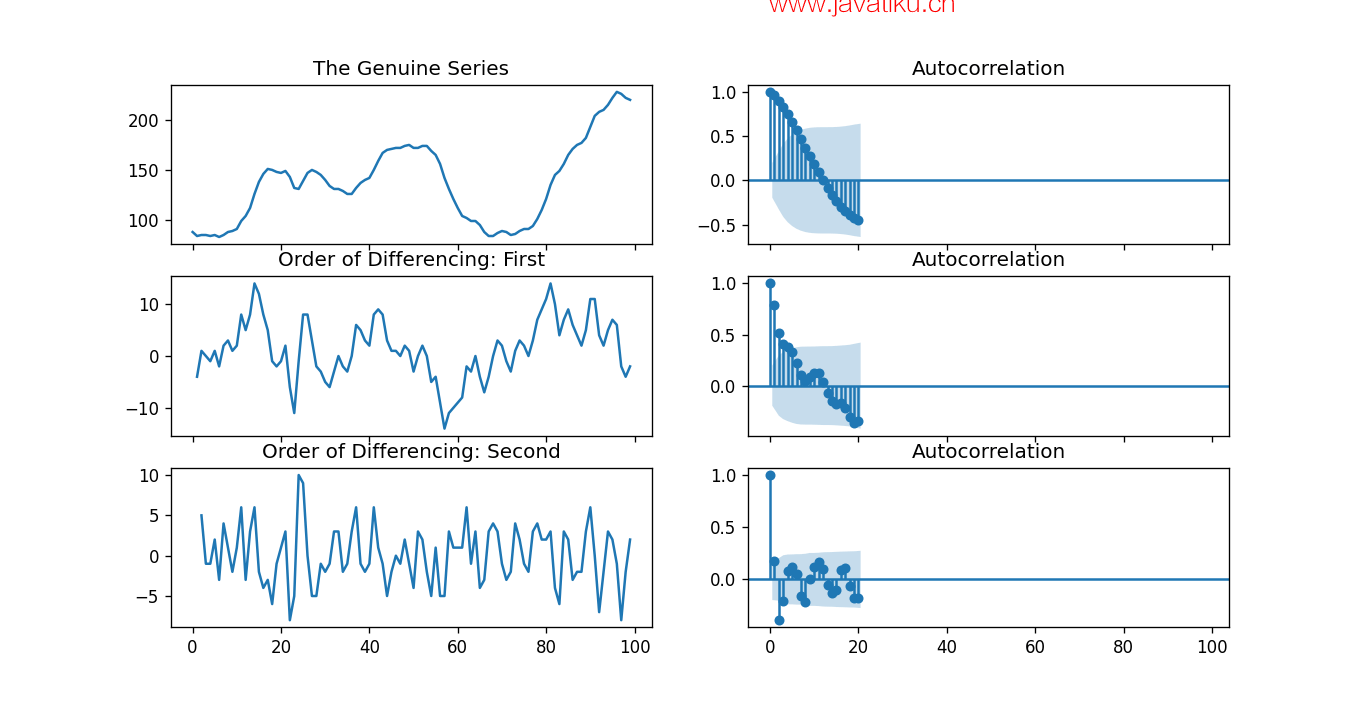
解释:
在上面的示例中,我们导入了所需的库和模块。然后,我们导入数据并绘制不同的图形。我们绘制了原始系列图、一阶差分和二阶差分,以及它们的自相关图。正如我们可以观察到的,时间序列已经通过两个差分阶数达到了稳定性。但是,当我们看二阶差分的自相关图时,滞后项迅速进入远离零的区域,表明系列可能已经过度差分。
因此,我们将临时修复差分阶数,因为该系列不是完全稳定的,或者可以说该系列具有弱稳定性。
这可以像下面这样完成。
示例:
from pmdarima.arima.utils import ndiffs
import pandas as pd
df = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
X = df.value
# Augmented Dickey Fuller Test
adftest = ndiffs(X, test = 'adf')
# KPSS Test
kpsstest = ndiffs(X, test = 'kpss')
# PP Test
pptest = ndiffs(X, test = 'pp')
print("ADF Test =", adftest)
print("KPSS Test =", kpsstest)
print("PP Test =", pptest) 输出:
ADF Test = 2
KPSS Test = 0
PP Test = 2解释:
在上面的示例中,我们导入了pmdarima模块的ndiffs方法。然后,我们导入数据集并将'X'定义为包含数据集值的对象。我们使用ndiffs方法执行ADF、KPSS和PP测试,并将其结果打印给用户。
查找自回归(AR)项(p)的阶数
在下面的部分中,我们将讨论检查模型是否需要任何自回归(AR)项的步骤。需要的AR项数量可以通过研究偏自相关(PACF)图来找到。
我们可以将偏自相关视为系列和其滞后之间的相关性,一旦我们排除了中间滞后的贡献。因此,PACF倾向于传达系列和其滞后之间的纯相关性。因此,我们可以确定自回归(AR)项中是否需要该滞后项。
一系列滞后k的偏自相关是Y的自回归方程中该滞后项的系数。
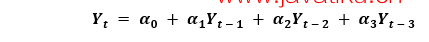
现在,让我们了解如何找到AR项的数量?
正如我们所知,稳态系列中的任何自相关都可以通过插入足够多的AR项来纠正。因此,我们可以最初将自回归(AR)项的阶数等于在PACF图中超过显著性限制的滞后数目。
示例:
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize':(9,3), 'figure.dpi':120})
# importing data
df = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
fig, axes = plt.subplots(1, 2, sharex = True)
axes[0].plot(df.value.diff()); axes[0].set_title('Order of Differencing: First')
axes[1].set(ylim = (0,5))
plot_pacf(df.value.diff().dropna(), ax = axes[1])
plt.show() 输出:
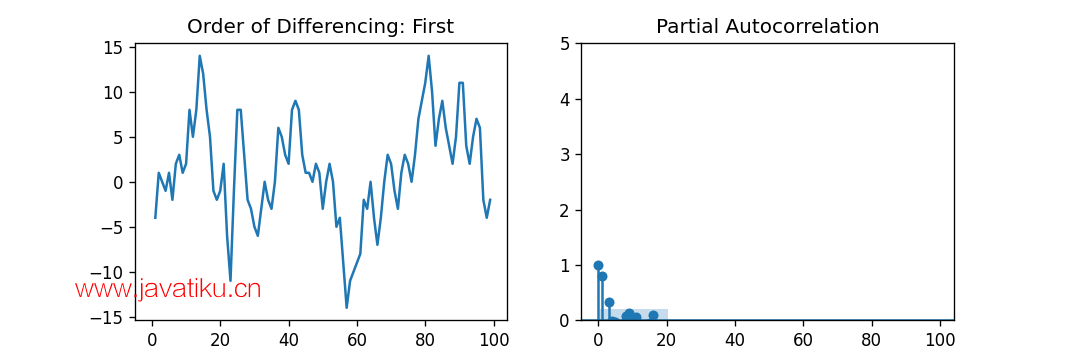
解释:
在上面的示例中,我们导入了所需的库、模块和数据集。然后,我们绘制了图形,代表了一阶差分及其偏自相关。
结果,我们可以观察到PACF滞后1在显著性线上方相当显著。滞后2也似乎相当显著,完全足够跨越显著性限制(蓝色区域)。然而,我们将保守地将p暂时设定为1。
查找移动平均(MA)项的阶数(q)
与我们之前在自回归(AR)项数量的偏自相关(PACF)图中所看到的类似,我们可以使用自相关(ACF)图来找到移动平均(MA)项的数量。移动平均(MA)项在理论上是滞后预测误差。
ACF图表示在稳态系列中去除自相关所需的移动平均(MA)项数量。
让我们考虑以下示例,以了解差分系列的自相关图。
示例:
import numpy as np, pandas as pd
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,3), 'figure.dpi' : 120})
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
fig, axes = plt.subplots(1, 2, sharex = True)
axes[0].plot(mydata.value.diff()); axes[0].set_title('Order of Differencing: First')
axes[1].set(ylim = (0, 1.2))
plot_acf(mydata.value.diff().dropna(), ax = axes[1])
plt.show() 输出:
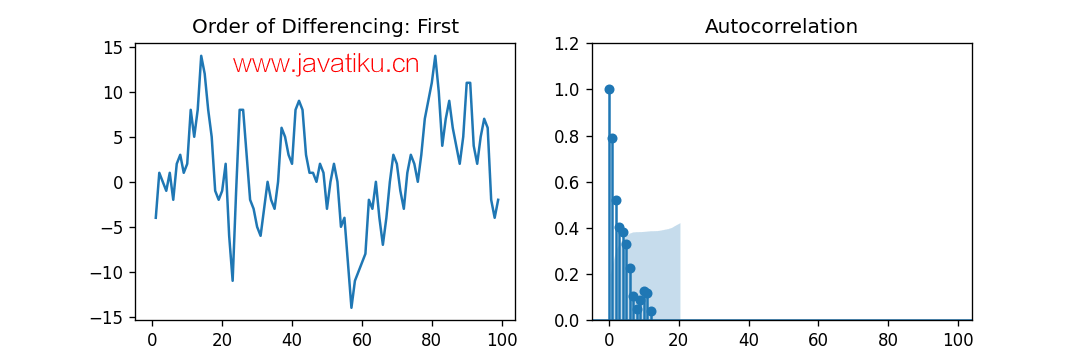
解释:
在上面的示例中,我们导入了所需的库、模块和数据集。然后,我们绘制了图形,代表了一阶差分及其自相关。结果,我们可以观察到某些滞后在显著性线上方相当显著。因此,我们可以临时将q固定为2。在存在任何疑虑的情况下,我们也可以使用更简单的模型,以充分展示Y。
处理略有欠差分或过度差分的时间序列
有时,可能会出现系列略有欠差分的情况,对其进行一次额外的差分会使系列略过度差分。在这种情况下,我们必须为略微欠差分的时间序列添加一个或多个额外的自回归(AR)项,为略微过度差分的时间序列添加额外的移动平均(MA)项。
一旦我们讨论了大多数主题,让我们开始创建用于时间序列预测的ARIMA模型。
构建ARIMA模型
一旦确定了p、q和d的值,我们将尝试创建ARIMA模型。下面是ARIMA()模块的实现示例:
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 2))
modelfit = mymodel.fit(disp = 0)
print(modelfit.summary())输出:
ARIMA Model Results
==============================================================================
Dep. Variable: D.value No. Observations: 99
Model: ARIMA(1, 1, 2) Log Likelihood -253.790
Method: css-mle S.D. of innovations 3.119
Date: Thu, 15 Apr 2021 AIC 517.579
Time: 21:10:37 BIC 530.555
Sample: 1 HQIC 522.829
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 1.1202 1.290 0.868 0.385 -1.409 3.649
ar.L1.D.value 0.6351 0.257 2.469 0.014 0.131 1.139
ma.L1.D.value 0.5287 0.355 1.489 0.136 -0.167 1.224
ma.L2.D.value -0.0010 0.321 -0.003 0.998 -0.631 0.629
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.5746 +0.0000j 1.5746 0.0000
MA.1 -1.8850 +0.0000j 1.8850 0.5000
MA.2 545.5472 +0.0000j 545.5472 0.0000
-----------------------------------------------------------------------------解释:
在上面的示例中,我们从statsmodels类中导入了新的ARIMA模块,并创建了阶数为1、1和2的ARIMA模型。然后,我们将模型的摘要打印给用户。正如我们可以观察到的,模型的概述显示了许多细节。中间的表格是系数表格,其中'coef'值充当相关项的权重。
我们还可以注意到,MA2项的系数趋向于零,而'P > |z|'列中的P-Value非常不显著。P-Value应小于0.05,理想情况下对应X的显著性。
现在,让我们尝试在不包括MA2项的情况下重新构建模型。
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 1))
modelfit = mymodel.fit(disp = 0)
print(modelfit.summary()) 输出:
ARIMA Model Results
==============================================================================
Dep. Variable: D.value No. Observations: 99
Model: ARIMA(1, 1, 1) Log Likelihood -253.790
Method: css-mle S.D. of innovations 3.119
Date: Thu, 15 Apr 2021 AIC 515.579
Time: 21:34:00 BIC 525.960
Sample: 1 HQIC 519.779
=================================================================================
coef std err z P>|z| [0.025 0.975]
---------------------------------------------------------------------------------
const 1.1205 1.286 0.871 0.384 -1.400 3.641
ar.L1.D.value 0.6344 0.087 7.317 0.000 0.464 0.804
ma.L1.D.value 0.5297 0.089 5.932 0.000 0.355 0.705
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.5764 +0.0000j 1.5764 0.0000
MA.1 -1.8879 +0.0000j 1.8879 0.5000
-----------------------------------------------------------------------------解释:
在上面的示例中,我们减小了模型的AIC,这实际上是很好的。我们还可以观察到AR1和MA1项的P-Value已经得到了改进,并且非常显著(<< 0.05)。
现在,让我们绘制残差,以确保没有常数均值和方差等模式。
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,3), 'figure.dpi' : 120})
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 1))
modelfit = mymodel.fit(disp = 0)
# Plotting Residual Errors
myresiduals = pd.DataFrame(modelfit.resid)
fig, ax = plt.subplots(1,2)
myresiduals.plot(title = "Residuals", ax = ax[0])
myresiduals.plot(kind = 'kde', title = 'Density', ax = ax[1])
plt.show()输出:
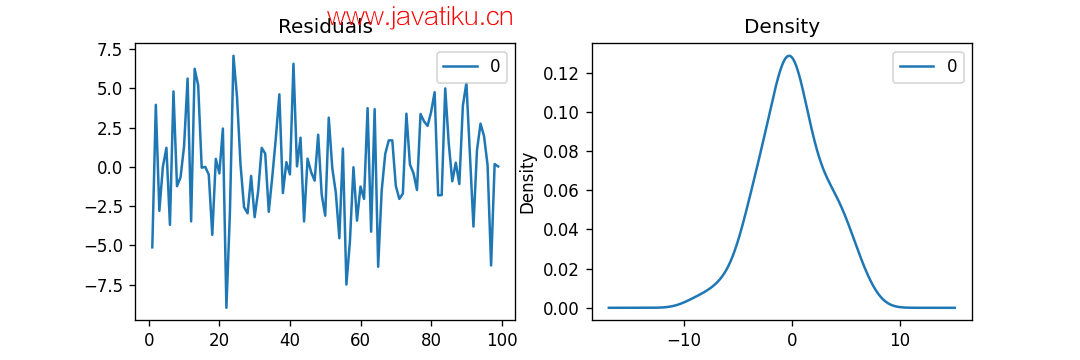
解释:
在上面的示例中,我们绘制了残差误差和密度图。我们可以观察到,残差误差看起来相当接近零均值和均匀方差。让我们使用plot_predict()函数绘制表示实际值与拟合值的图形,通过该函数,可以确保没有模式。
示例:
import numpy as np, pandas as pd
from statsmodels.tsa.arima_model import ARIMA
import matplotlib.pyplot as plt
plt.rcParams.update({'figure.figsize' : (9,3), 'figure.dpi' : 120})
# importing data
mydata = pd.read_csv('mydataset.csv', names = ['value'], header = 0)
# Creating ARIMA model
mymodel = ARIMA(mydata.value, order = (1, 1, 1))
modelfit = mymodel.fit(disp = 0)
# Actual vs Fitted
modelfit.plot_predict(dynamic = False)
plt.show()输出:
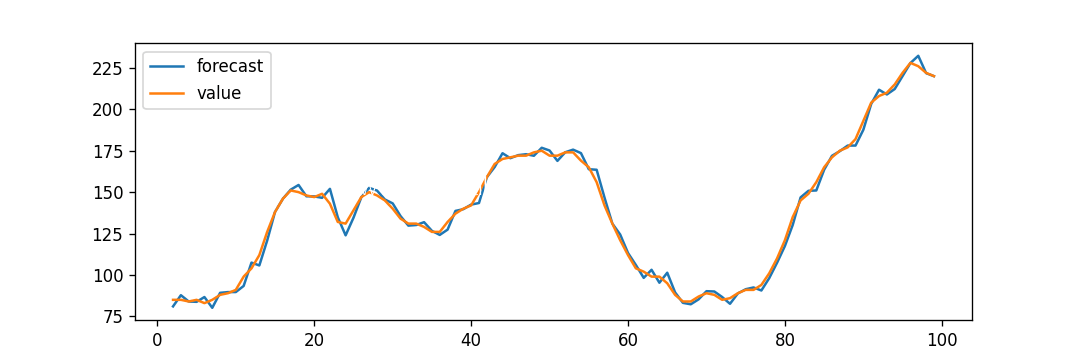
解释:
在上面的示例中,我们现在绘制了'实际与拟合'图,并设置dynamic = False。因此,用于预测的是样本内滞后值。
因此,模型在过去的值使下一个预测之前得到了训练。因此,它可以创建拟合预测,而实际值看起来非常灵敏。



