Python教程-Python中的两个数字的最大公约数

最大公约数（GCD）是一个数学术语，用于找到可以完全除尽两个数字的最大公因数。GCD也被称为最高公共因子（HCF）。例如，两个数字54和24的HCF/GCD是6。因为6是可以完全除尽54和24的最大公约数。

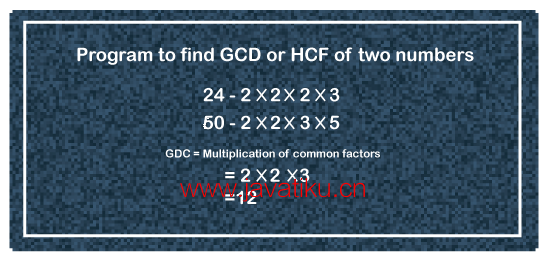
使用gcd()函数计算最大公约数

在Python中，gcd()是由math模块提供的内置函数，用于找到两个数字的最大公约数。

语法

gcd(a, b) 

其中a和b是作为参数传递给gcd()函数的两个整数。

让我们创建一个程序，使用Python中的math.gcd()内置函数来打印两个数字的最大公约数。

math_fun.py

# create a program to print the gcd of two number in python using the math.gcd() function.  
import math  
print(" GCD of two number 0 and 0 is ", math.gcd(0, 0)) #math.gcd(a, b), a and b are the two integer number  
print(" GCD of two number 0 and 48 is ", math.gcd(0, 48))  
a = 60 # assign the number to variable a  
b = 48 # assign the number to variable b  
print(" GCD of two number 60 and 48 is ", math.gcd(a, b)) # pass the variable a and b to math.gcd() function.  
print(" GCD of two number 48 and -12 is ", math.gcd(48, -12)) # pass the integer number  
print(" GCD of two number -24 and -18 is ", math.gcd(-24, -18))  
print(" GCD of two number -60 and 48 is ", math.gcd(-60, 48))  

输出:

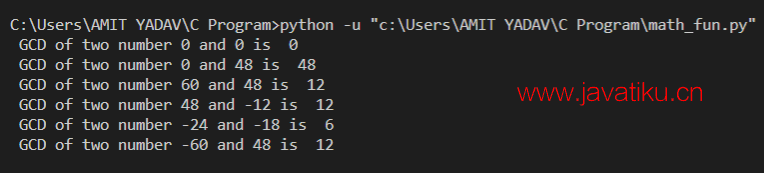
在上面的示例中，math.gcd()函数生成了给定两个数字的最大公约数。在gcd()函数中，a和b作为参数传递，它返回两个整数数字的最大公约数，完全除尽这些数字。

使用递归计算最大公约数

递归是Python中定义的一种占用内存的函数，通过自引用表达式调用自身。这意味着函数将不断调用和重复自身，直到满足定义的条件以返回数字的最大公约数。

算法的伪代码

步骤1：从用户获取两个输入，x和y。

步骤2：将输入数字作为参数传递给递归函数。

步骤3：如果第二个数字等于零（0），则返回第一个数字。

步骤4：否则，它会递归调用函数，以第二个数字作为参数，直到获取能够将第二个数字除以第一个数字的余数。

步骤5：将gcd_fun()调用或分配给一个变量。

步骤6：显示两个数字的最大公约数。

步骤7：退出程序。

让我们理解使用递归来查找两个数字的最大公约数的程序。

gcdRecur.py

# write a program to understand the GCD of two number in python using the recursion.  
def gcd_fun (x, y):  
    if (y == 0): # it divide every number  
        return x  # return x  
    else:  
        return gcd_fun (y, x % y)  
x =int (input ("Enter the first number: ")) # take first no.   
y =int (input ("Enter the second number: ")) # take second no.   
num = gcd_fun(x, y) # call the gcd_fun() to find the result  
print("GCD of two number is: ")  
print(num) # call num 

输出:

使用循环计算最大公约数

让我们创建一个程序，使用循环来查找Python中两个数字的最大公约数。

gcdFile.py

def GCD_Loop( a, b):  
    if a > b:  # define the if condition  
        temp = b  
    else:  
        temp = a  
    for i in range(1, temp + 1):  
        if (( a % i == 0) and (b % i == 0 )):  
            gcd = i  
    return gcd  
x = int(input (" Enter the first number: ") ) # take first no.   
y =int (input (" Enter the second number: ")) # take second no.   
num = GCD_Loop(x, y) # call the gcd_fun() to find the result  
print("GCD of two number is: ")  
print(num) # call num  

输出:

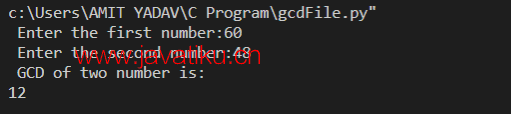
如上面的程序所示，我们将两个值作为输入，并将这些数字传递给GCD_Loop()函数以返回最大公约数。

使用欧几里德算法计算最大公约数

欧几里德算法是一种高效找到两个数字最大公约数的方法。这是最古老的算法，将较大的数除以较小的数并取余数。然后，它再次用余数除以较小的数，这个算法不断地除以数字，直到余数变为0。

例如，假设我们要计算两个数字60和48的H.C.F。然后我们将60除以48，它返回余数12。现在我们再次将数字24除以12，然后它返回余数0。所以，这样我们得到H.C.F为12。

欧几里德算法的伪代码

步骤1：有两个整数，例如a和b。

步骤2：如果a = 0，则GCD(a, b)为b。

步骤3：如果b = 0，则GCD(a, b)为a。

步骤4：a mod b找到

步骤5：假设a = b和b = R

步骤6：重复步骤4和步骤3，直到a mod b等于或大于0。

步骤7：GCD = b，然后打印结果。

步骤8：停止程序。

让我们使用Python中的欧几里德算法找到两个数字的H.C.F或GCD。

Euclid.py

# Create a program to find the GCD of two number in python using the Euclid's Algorithm.  
def find_hcf(a,b):  
    while(b):  
        a, a = b, a % b  
        return a  
a = int(input (" Enter the first number: ") ) # take first no.   
b = int(input (" Enter the second number: ")) # take second no.   
num = find_hcf(a, b) # call the find_hcf() to get the result  
print("  The HCF of two number a and b is ")  
print(num) # call num  

输出: