PyTorch 教程-在 PyTorch 中测试深度神经网络

我们将绘制一个精确的决策边界来分离我们的分类结果。在此,我们还将测试我们的模型。训练模型的步骤如下:
步骤 1:
在第一步中,我们定义一个名为 plot_decision_boundary() 的函数,该函数包含两个参数:训练数据 x 和标签 y。这个函数将返回决策边界的等高线图。
def plot_decision_boundary(x, y): 步骤 2:
在这一步中,我们定义一个网格,以正确覆盖我们的数据。过程从定义数据集中 x 和 y 坐标的跨度开始。x_span 和 y_span 将定义为50个等间距点:
x_span=np.linspace(min(x[:,0]),max(x[:,0]))
y_span=np.linspace(min(y[:,1]),max(y[:,1])) 步骤 3:
接下来,我们将定义变量 xx 和 yy。变量 xx 和 yy 存储一个从 numpy 的 meshgrid() 函数获取的正方形二维数组。
xx,yy=np.meshgrid(x_span,y_span) meshgrid() 函数接受向量 x_span 和 y_span 作为参数。这两个向量都包含50个元素,这个函数将返回一个 50x50 矩阵的二维数组。新添加的行将是 x_span 向量中原始行的重复副本,并返回给 xx 变量。y_span 的过程相同;它将返回一个 50x50 矩阵的二维数组,其中新添加的列将是 y_span 向量中原始列的重复副本。这个矩阵将返回给 yy 变量。
步骤 4:
借助这些新创建的矩阵 xx 和 yy,我们将创建一个覆盖整个数据集的笛卡尔网格。为此,我们首先需要使用 ravel() 方法将 xx 和 yy 矩阵转换为一维。
print(xx.ravel(),yy.ravel()) 步骤 5:
现在,我们有50个 x 坐标,为了定义我们的网格,我们需要以列 y 的排列方式将这些数组连接起来。这可以通过 c_[] 实现。
grid=np.c_[xx.ravel(),yy.ravel()] 现在,我们将使用 torch.Tensor() 将它们转换为张量。这将把我们的 50x50 网格转换为张量数据。
grid=torch.Tensor(np.c_[xx.ravel(),yy.ravel()]) 步骤 6:
现在,我们终于可以使用 model.forward(),并将网格作为唯一参数。通过将整个网格张量输入 model.forward() 函数,训练过的模型将测试我们 50x50 网格内的所有点,这将返回一个预测的张量。
model.forward(grid) 这个预测表示任何给定点被标记为 1 的概率,我们将这个张量存储在一个名为 pred_func 的变量中。
pred_func=model.forward(grid) 步骤 7:
现在,我们将重新塑造 pred_func,使其与我们原始的 xx 和 yy 维度具有相同的形状。
z=pred_func.view(xx.shape).numpy() 这将产生一个错误;我们将使用 detach 方法,该方法排除了与 pred_func 的值相关联的梯度计算的任何子图。
z=pred_func.view(xx.shape).detach().numpy() 步骤 8:
现在,我们的下一步是将我们的预测结果与它们相应的坐标对应起来。为此,我们将使用 plt.contourf(),它将创建一个包含 xx、yy 和 z 的预测结果的等高线图。
plt.contourf(xx, yy,z) 步骤 9:
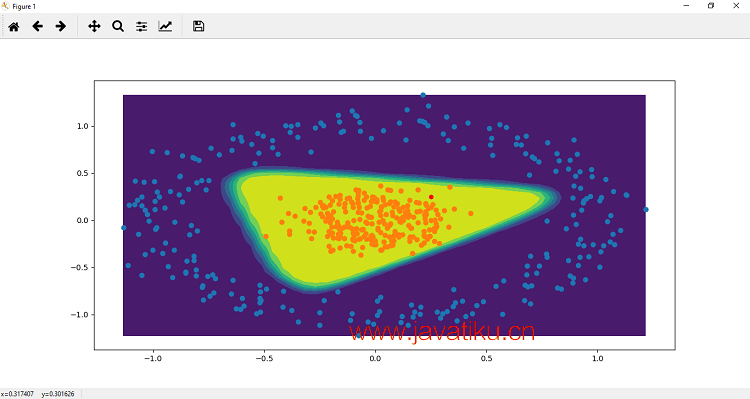
现在,我们将首先调用 plot_decision_boundary() 方法,然后调用我们之前定义的 scatter_plot() 方法。这将可视化我们的数据:
plot_decision_boundary(x,y)
scatter_plot() 
步骤 10:
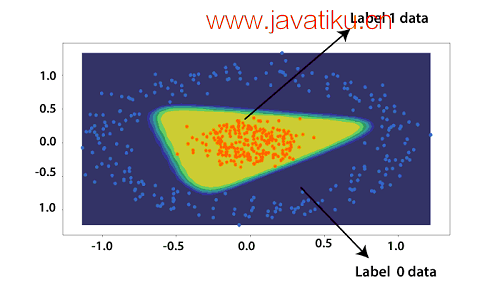
我们将重新绘制我们拟合的模型,为此,我们将对我们初始化的一个随机点进行预测。我们将选择两个点来更好地理解
p1=torch.Tensor(0.25,0.25]) 步骤 11:
现在,下一步是为了可视化目的绘制这个点,这样我们就可以确定这个点属于类别 1 还是 0。
plt.plot(p1[0],p1[1],marker='o',markersize=5,color='red') 点 p1 最初是张量的形式,所以我们通过类型转换将这个点变成 numpy。
plt.plot(p1.numpy()[0],p1.numpy()[1],marker='o',markersize=5,color='red') 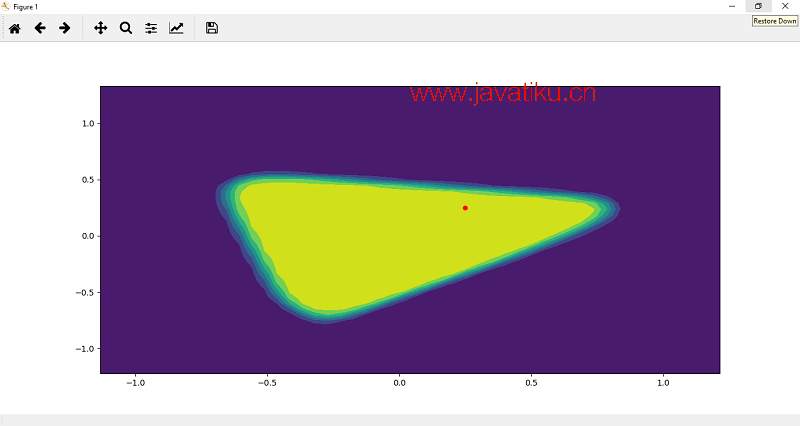
步骤 12:
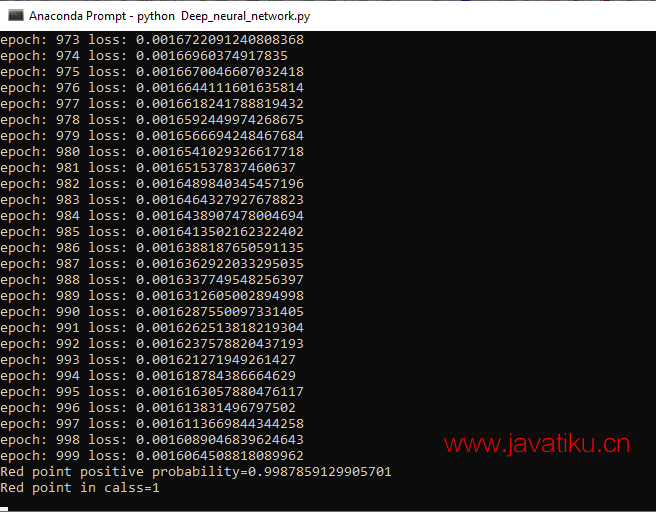
我们可以对这个点进行预测。我们将预测这个点属于正区域 2 类别 1 的概率。我们知道所有橙色的点都被标记为 1,所有蓝色的点都被标记为 0。因此,概率可以确定为
print("Red point positive probability={}".format(model.forward(p1).item())) 
步骤 13:
现在,我们将回到我们的类初始化,并创建一个名为 predict 的方法,该方法有一个参数。我们使用 self.forward(x) 来找出概率。如果概率大于 0.5,则返回类别 1,否则返回 0。
def predict(self,x):
pred=self.forward(x)
if pred>=0.5:
return 1
else:
return 0 步骤 14:
最后,我们将添加一个打印语句,告诉我们使用 predict 方法的类别为
print("Red point in calss={}".format(model.predict(p1))) 
我们的模型运行顺利,并能准确地处理随机数据。
完整代码
import torch
import numpy as np
import matplotlib.pyplot as plt
import torch.nn as nn
from sklearn import datasets
no_of_points=500
x,y=datasets.make_circles(n_samples=no_of_points,random_state=123,noise=0.1,factor=0.2)
xdata=torch.Tensor(x)
ydata=torch.Tensor(y)
def scatter_plot():
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()
class Deep_neural_network(nn.Module):
def __init__(self,input_size, h1, output_size):
super().__init__()
self.linear=nn.Linear(input_size, h1) # input layer connect with hidden layer
self.linear1=nn.Linear(h1, output_size) # hidden layer connect with output layer
def forward(self,x):
x=torch.sigmoid(self.linear(x)) # Return the prediction x
x=torch.sigmoid(self.linear1(x)) # Prediction will go through the next layer.
return x # Returning final outputs
def predict(self,z):
pred=self.forward(z)
if pred>=0.5:
return 1
else:
return 0
torch.manual_seed(2)
model= Deep_neural_network(2,4,1) # 2 input nodes, 4 hidden nodes and 1 output node
print(list(model.parameters()))
criterion=nn.BCELoss()
optimizer=torch.optim.Adam(model.parameters(),lr=0.1)
epochs=1000
losses=[]
for i in range(epochs):
ypred=model.forward(xdata)
loss=criterion(ypred,ydata)
print("epoch:",i,"loss:",loss.item())
losses.append(loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
def plot_decision_boundary(x, y):
x_span=np.linspace(min(x[:,0]),max(x[:,0]))
y_span=np.linspace(min(x[:,1]),max(x[:,1]))
xx,yy=np.meshgrid(x_span,y_span)
grid=torch.Tensor(np.c_[xx.ravel(),yy.ravel()])
pred_func=model.forward(grid)
z=pred_func.view(xx.shape).detach().numpy()
plt.contourf(xx,yy,z)
z1=0.25
z2=0.25
p1=torch.Tensor([z1,z2])
plt.plot(p1.numpy()[0],p1.numpy()[1],marker='o',markersize=5,color='red')
print("Red point positive probability={}".format(model.forward(p1).item()))
print("Red point in calss={}".format(model.predict(p1)))
plot_decision_boundary(x,y)
scatter_plot()