PyTorch 教程-深度神经网络中的反向传播过程

反向传播是神经网络的一个重要概念。我们的任务是尽可能准确地分类数据。为此,我们需要更新参数的权重和偏差值,但在深度神经网络中,我们如何做到这一点?在线性回归模型中,我们使用梯度下降来优化参数。类似地,在这里我们也使用梯度下降算法,结合反向传播。
对于单个训练样本,反向传播算法计算误差函数的梯度。反向传播可以写成神经网络的一个函数。反向传播算法是一组方法,用于有效地训练人工神经网络,遵循梯度下降方法,利用链式法则。
反向传播的主要特点是迭代、递归和高效的方法,通过这种方法计算更新的权重,以改进网络,直到它能够执行其正在训练的任务。网络设计时需要知道激活函数的导数,这是反向传播所需的。
那么,误差函数在反向传播中是如何使用的,反向传播是如何工作的呢?让我们从一个例子开始,通过数学方式来理解反向传播如何准确地更新权重。
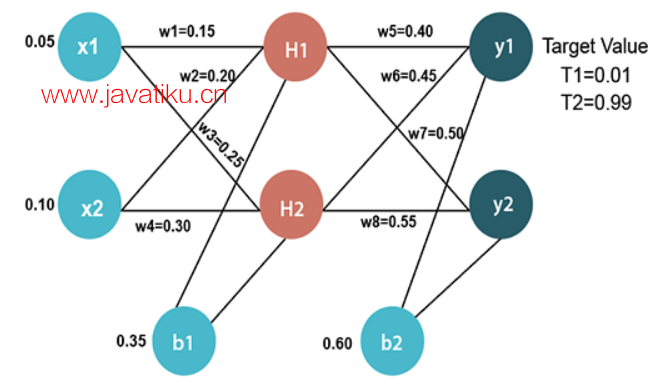
输入值
X1=0.05 X2=0.10
初始权重
W1=0.15 W2=0.20 W3=0.25 W4=0.30 w5=0.40 w6=0.45 w7=0.50 w8=0.55
偏差值
b1=0.35 b2=0.60
目标值
T1=0.01 T2=0.99
现在,我们首先通过前向传播计算H1和H2的值。
前向传播
为了找到H1的值,我们首先将输入值与权重相乘:
H1=x1×w1+x2×w2+b1 H1=0.05×0.15+0.10×0.20+0.35 H1=0.3775
为了计算H1的最终结果,我们执行了Sigmoid函数:

我们将以与H1相同的方式计算H2的值:
H2=x1×w3+x2×w4+b1 H2=0.05×0.25+0.10×0.30+0.35 H2=0.3925
为了计算H2的最终结果,我们执行了Sigmoid函数:

现在,我们将以与计算H1和H2相同的方式计算y1和y2的值。
为了找到y1的值,我们首先将输入值(即H1和H2的结果)与权重相乘:
y1=H1×w5+H2×w6+b2 y1=0.593269992×0.40+0.596884378×0.45+0.60 y1=1.10590597
为了计算y1的最终结果,我们执行了Sigmoid函数:

我们将以与y1相同的方式计算y2的值:
y2=H1×w7+H2×w8+b2 y2=0.593269992×0.50+0.596884378×0.55+0.60 y2=1.2249214
为了计算y2的最终结果,我们执行了Sigmoid函数:

我们的目标值是0.01和0.99。我们的y1和y2值与我们的目标值T1和T2不匹配。
现在,我们将找到总误差,即输出与目标输出之间的差异。总误差计算如下:

因此,总误差是:

现在,我们将通过反向传播来更新权重。
输出层的反向传播
为了更新权重,我们计算每个权重对应的误差,以帮助总误差。权重w的误差是通过对总误差求w的偏导数来计算的。

我们执行反向过程,首先考虑最后一个权重w5:

从方程二可以清楚地看到,我们不能对w5进行偏导数计算,因为没有w5。我们将方程一分成多个项,以便我们可以轻松地对w5求导:
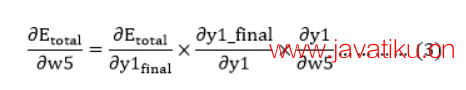
现在,我们一项一项地计算,以对w5求导:

将e-y的值放入方程式(5)中:

因此,我们将

的值放入方程式3中,找到最终结果。

现在,我们将使用以下公式计算更新后的权重w5new:

同样的方式,我们计算w6new、w7new和w8new,得到以下值:
w5new=0.35891648 w6new=408666186 w7new=0.511301270 w8new=0.561370121
隐藏层的反向传播
现在,我们将进行反向传播到我们的隐藏层,并更新权重w1、w2、w3和w4,就像我们对w5、w6、w7和w8权重所做的那样。
我们将计算w1处的误差为

从方程(2)可以看出,我们无法对w1进行偏导数分解,因为没有w1。我们将方程(1)拆分为多个项,以便我们可以轻松地对w1进行偏导数分解,如下所示
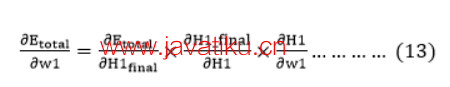
现在,我们逐一计算每个项,对w1进行偏导数分解
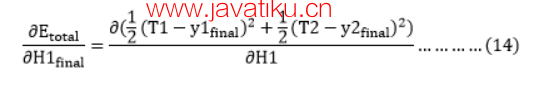
我们再次拆分,因为在Etoatal中没有H1final项,拆分如下
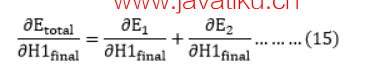

再次拆分,因为在E1和E2中没有H1项。 拆分如下

我们再次拆分
因为在E1和E2中没有y1和y2项。 拆分如下
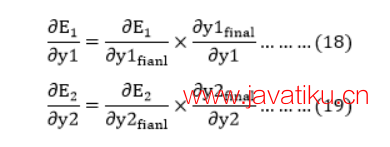
现在,通过将值放入方程(18)和(19)中,我们找到了
的值
从方程(18)得到

从方程(8)得到
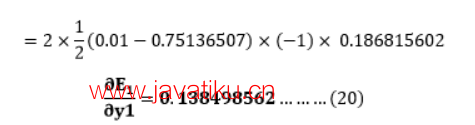
从方程(19)得到

将e-y2的值放入方程(23)中

从方程(21)得到

现在从方程(16)和(17)得到

将

的值放入方程(15)中

我们有
我们需要找出
如

将e-H1的值放入方程(30)中

我们计算总输入到H1的偏导数,与我们对输出神经元所做的方式相同:

因此,我们将
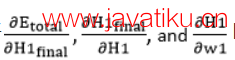
的值放入方程(13)中找到最终结果。

现在,我们将使用以下公式计算更新后的权重w1new
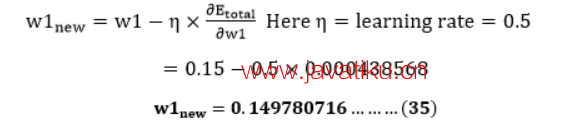
以相同的方式,我们计算w2new,w3new和w4new,得到以下值
w1new=0.149780716 w2new=0.19956143 w3new=0.24975114 w4new=0.29950229
我们已经更新了所有的权重。当我们向网络输入0.05和0.1时,我们发现了0.298371109的误差。在第一轮反向传播中,总误差降至0.291027924。经过10000次重复此过程后,总误差降至0.0000351085。此时,当我们向前馈送0.05和0.1时,输出神经元生成0.159121960和0.984065734,即接近我们的目标值。



