Scratch编程教程-Scratch画笔艺术：绘制正多边形

正多边形是指所有边和角都相等的多边形。它是一种简单的多边形，也是最常见的基本几何形状。

任务描述

本文将介绍如何通过Scratch编程绘制任意边数的正多边形，例如正方形、正五边形、正六边形等。

编程思路

编程思路很简单，只需要确定正多边形的边长和转角，每绘制完一条线段，就调整画笔方向，再绘制下一条线段，直至完成整个正多边形。

程序设计

为了更好地理解绘制的方法和过程，我们先编写一个程序绘制常见的正方形和正五边形，最后再实现任意正多边形的绘制。

1.绘制正方形

Scratch中的画笔模块为角色提供了与画图相关的功能和指令，只需要让角色在舞台上移动，就可以在舞台上画出移动轨迹。让我们来看一个简单的绘制直线程序示例，如下图所示：

当点击绿旗时，小猫向前移动了100步，同时在舞台上画出了一条蓝色的运动轨迹，如下图所示：

这就如同角色手握一只画笔，再添加积木块“落笔”之后，角色就可以根据程序的指令在舞台上绘制图形。

既然能够绘制一条直线，那么绘制正方形当然不在话下。为了更好地演示角色面向的方向，我们选择了一个小甲壳虫角色。

由于正方形有4条边，4个直角都为90度，因此我们只需要让角色移动一段距离之后，向右旋转90度，再移动一段相同的距离，向右旋转90度，以此类推，让甲壳虫移动、旋转4次，就可以绘制一个完美的正方形了。程序非常的简单，如下图所示：

在绘制之前，我们需要进行一些初始化的工作，包括：

• 将甲壳虫移到(-50，50)坐标处，确保绘制的图案处于舞台中心。这个不是必须的，可以根据需要进行设置。
• 将角色面向90度，让甲壳虫沿着90度方向开始移动绘制。
• 将舞台上绘制的内容全部擦除，确保每次绘制之前清空之前的内容。

点击绿旗按钮，执行程序，绘制出的正方形效果如下：

[小技巧]：在右转90度指令的下方，添加一个等待1秒指令，可以更清楚地观察绘制的过程。你可以试试看。

2.绘制正五边形

既然正方形已经绘制好了，正五边形也就容易了。在刚刚的程序上稍作修改就可以绘制正五边形。不过，首先我们必须明确两个问题：

• 正五边形有几条边？
• 每次旋转多少度呢？

针对第一个问题，简单到不能再简单了，正五边形当然是5条边了，所以重复的次数设置为5次就可以了，移动的步数决定了边长的长度，这里就不再修改，继续使用100步。

针对第二个问题，每次旋转的角度是多少呢？我们一起来分析一下，话说，任意多边形的外角和都是360度，无论是三角形、四边形还是十边形，它们的外角和都是360度。那么正五边形的外角和是多少度呢？当然是360度啦。

你可能会问了，外角是谁，我不认识啊。且听我说来，如下图所标注的角都是外角，所有的外角度数相加是360度。而正多边形的每一个外角度数都是相等的，对于正五边形来说，每一个外角的度数是360 / 5 = 72度。

因此，角色每移动100步，向右旋转72度即可，绘制正五边形的完整程序如下图所示，标红部分表示修改的部分：

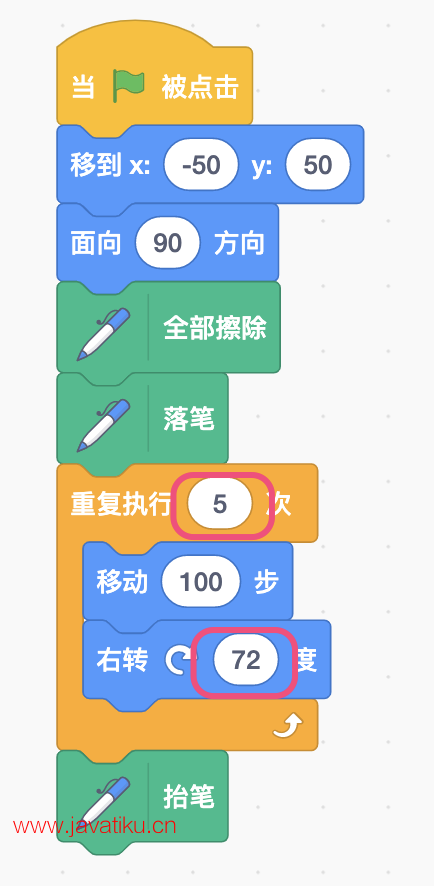
运行程序，甲壳虫依然很快就画出了一个标准的正五边形，如图：

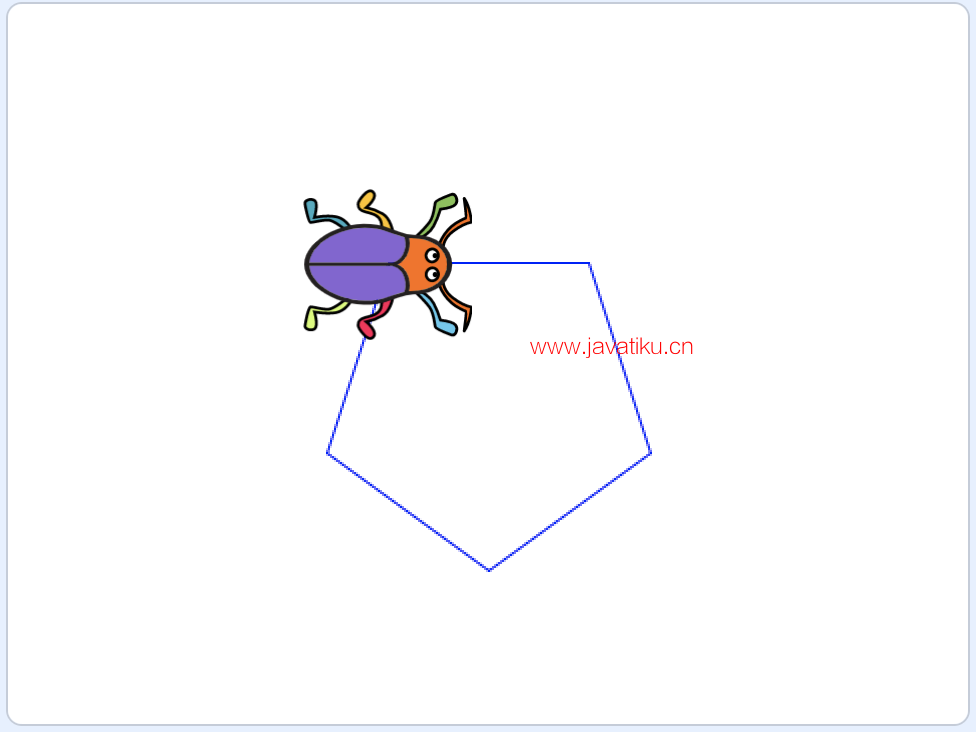
绘制正五边形效果

3.绘制任意正多边形

你可能已经注意到，绘制正方形和正五边形的程序有很多相似之处，只有两个小的差别。你可能在考虑如何绘制不同的正多边形，但其实程序是相似的，我们只需要注意旋转角度和边长的大小。

例如，对于正三角形，它的每个外角都是360/3=120度，因此每次移动一定距离后需要旋转120度。对于正十二边形，每个外角是360/12=30度，因此每次移动一定距离后需要旋转30度。然而，随着边数的增加，移动距离应该相应减小，否则会产生奇怪的图形，如下图所示：

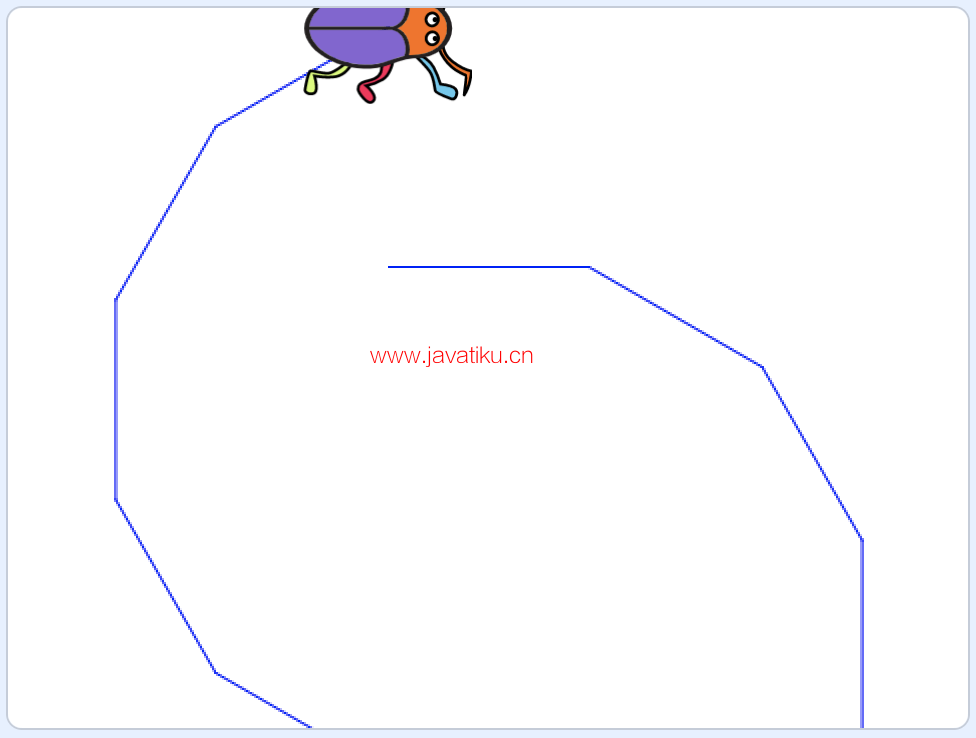
角色的绘制被舞台边缘阻挡

这是为什么呢？原因是舞台的边缘阻挡了角色的运动，改变了它正常的运动轨迹。解决这个问题的方法是适当减小边长，比如将它改为60步。程序如下所示：

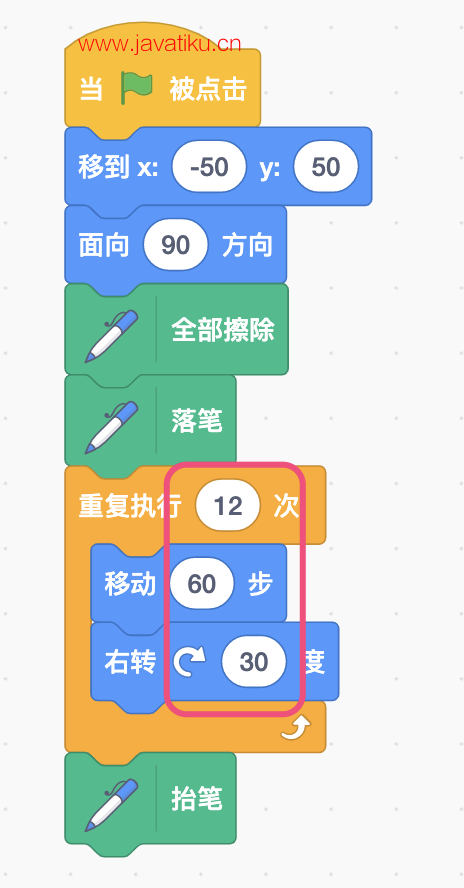
绘制正十二边形的程序

再次运行程序，这一次就完全正常了，如下图所示：

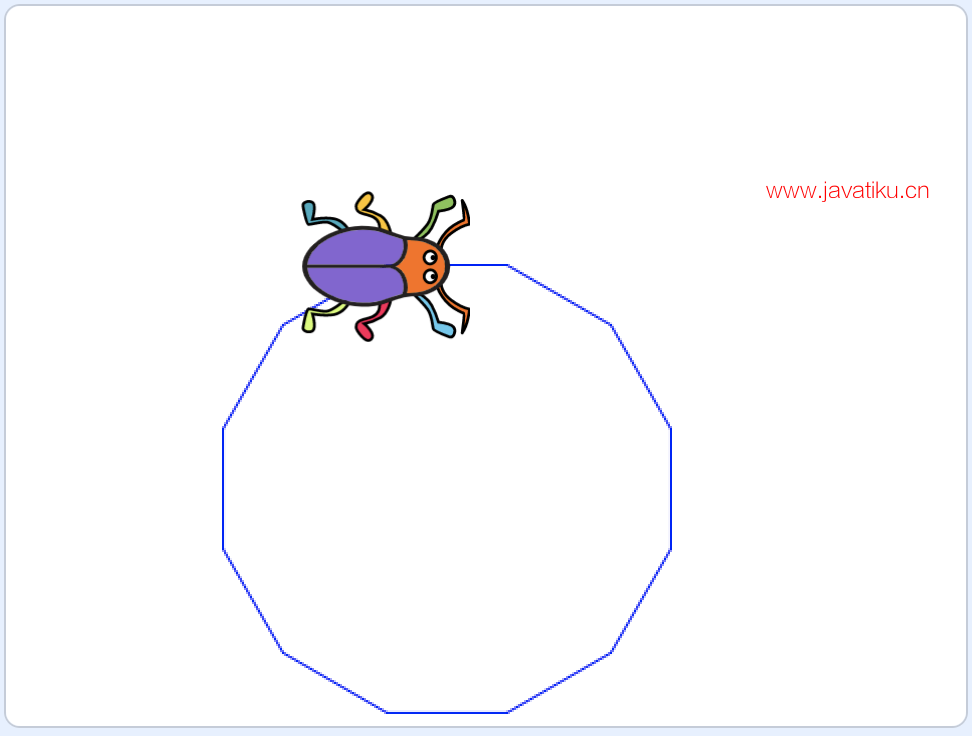
绘制正十二边形的效果

对于不同的正多边形，绘制流程是相同的，只有3个地方需要修改：

• 重复的次数，它决定正多边形的边数
• 移动的步数，它决定边长的大小
• 旋转的角度

其中，旋转角度和边数之间的关系是二者的乘积为360，即边数*旋转角度=360度。边长也与边数有关，边数越多，边长应越小，二者成反比例关系。为了简化程序，我们可以使用运算类积木块优化刚才的程序，优化后的程序如下所示：

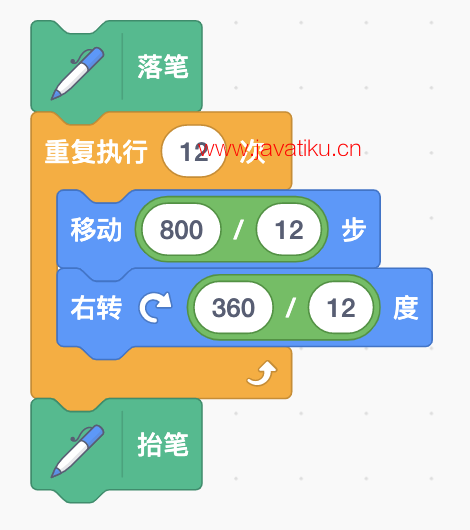
绘制正十二边形的优化代码

其中，移动步数使用了800/边数，这保证了当边数较少时，边长较大，当边数较多时，边长变短。这种方法非常灵活，当然，800是经过多次测试得到的，可以根据实际情况进行调整。

因此，我们可以使用这个程序绘制任意正多边形，只需要改变边数就可以了，其他部分不需要修改。有了这个程序，我们可以自由绘制需要的任意正多边形。等到学会制作自制积木时，我们可以将整个功能做成自制积木