Python教程-在Python中的堆排序

堆排序与选择排序相似，它们都是找到最大元素并将其放在末尾的排序算法。堆排序是一种基于二叉堆数据结构的比较排序算法，是高效排序算法的最佳示例。

什么是堆排序？

堆排序是一种高效且流行的排序算法。堆排序的概念是逐个从列表的堆部分“消除”元素并将它们插入到已排序的部分。在深入了解堆排序算法之前，让我们讨论一下堆数据结构。

它是一种原地算法，这意味着用于存储排序后的列表的内存量是固定的，或者内存大小不依赖于初始列表的大小。

例如 - 我们不需要额外的内存堆栈来存储已排序的数组，也不需要递归调用堆栈。堆排序算法通常使用第二个数组来对固定值进行排序。这个过程快速、简单、自然且易于实现。

另一方面，堆排序是不稳定的，这意味着它不会保持具有相等值的元素的比较顺序。它可以快速排序原始类型，如整数和字符，但在处理复杂类型和对象时存在问题。

让我们通过以下示例来理解 -

我们有一个自定义类Student，具有age和name属性，以及数组中该类的多个对象，包括一个名为"Thomas"、年龄为20的学生，还有"Peter"，也是20岁，并按照相同的顺序出现。

如果我们按年龄对人的数组进行排序，那么不能保证"Thomas"会在排序后的数组中出现在"Peter"之前。它可以被定义的顺序，但没有保证。

堆数据结构

堆数据结构是满足堆属性的完全二叉树。它也被称为二叉堆。

完全二叉树满足以下属性。

• 每个级别都应该填满。
• 所有节点尽量在最左边。

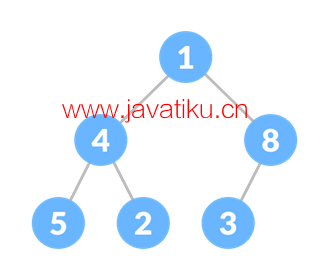
如上图所示，堆的图像中，但它没有排序。在本文中，我们不会深入研究堆，因为我们的重点是解释堆排序算法，而不是堆。在堆排序中，下一个最小的元素总是第一个元素。

堆树可以是两种类型 - 最小堆和最大堆。最小堆记录最大元素。最大堆记录最大元素。堆主要支持以下操作 - delete_minimum()、get_minimum() 和 add()。

堆的第一个元素在恢复后可以删除。它需要O(log N)的时间，这非常有效。

实现

Python提供了使用堆排序来排序元素的内置函数。以下是这些函数。

• heappush(list, item) - 用于添加堆元素并重新排序它。
• heappop(list) - 用于删除元素并返回元素。
• heapfy() - 用于将给定的列表转化为堆。

考虑以下堆排序的示例。

示例 -

from heapq import heappop, heappush  
   
 def heapsort(list1):  
     heap = []  
     for ele in list1:  
         heappush(heap, ele)  
   
     sort = []  
   
     # the elements are lift in the heap  
     while heap:  
         sort.append(heappop(heap))  
   
     return sort  
   
 list1 = [27, 21, 55, 15, 60, 4, 11, 17, 2, 87]  
 print(heapsort(list1))  

输出：

[2, 4, 11, 15, 17, 21, 27, 55, 60, 87]

解释：

在上面的代码中，我们导入了heapq模块，其中包含heappop()和heappush()方法。我们创建了heapsort()方法，它以list1作为参数。使用for循环迭代list1，并将元素推入空堆中。我们使用while循环，将排序后的元素添加到空排序中。

我们调用了heapsort()函数并传入一个列表。它返回了已排序的列表。

对自定义对象进行排序

堆排序对于预定义的数据类型非常有用，但处理用户定义的数据类型（例如类对象）更复杂。我们将在本节中对自定义对象进行排序。

正如我们所看到的，我们的实现依赖于内置方法。Python提供了以下方法。

• heapq.nlargest(n, iterable, key = None) - 该方法用于从可迭代的数据集中获取包含前n个最大元素的列表。
• heapq.nsmallest(n, iterable, key = None) - 该方法用于从可迭代的数据集中获取包含前n个最小元素的列表。

让我们了解自定义对象的以下实现。

示例 -

from heapq import heappop, heappush  
   
 class Car:  
     def __init__(self, model, year):  
         self.model = model  
         self.year = year  
   
     def __str__(self):  
         return str.format("Model Name: {}, Year: {}", self.model, self.year)  
   
     def __lt__(self, other):  
         return self.year < other.year  
   
     def __gt__(self, other):  
         return other.__lt__(self)  
   
     def __eq__(self, other):  
         return self.year == other.year  
   
     def __ne__(self, other):  
         return not self.__eq__(other)  
   
   
 def heapsort(list1):  
     heap = []  
     for element in list1:  
         heappush(heap, element)  
   
     ordered = []  
   
     while heap:  
         ordered.append(heappop(heap))  
   
     return ordered  
   
   
 car1 = Car("Renault", 2001)  
 car2 = Car("Bentley", 2005)  
 car3 = Car("Kia", 2014)  
 car4 = Car("Maruti Suzuki", 1999);  
 car5 = Car("Nano", 2012)  
   
 list1 = [car1, car2, car3, car4, car5]  
   
 for c in Heapsort Heapsort (list1):  
     print(c)  

输出：

Model Name: Maruti Suzuki, Year: 1999
Model Name: Renault, Year: 2001
Model Name: Bentley, Year: 2005
Model Name: Nano, Year: 2012
Model Name: Kia, Year: 2014

我们已根据年份对对象进行排序。

堆排序与其他算法的比较

另一种流行的快速排序算法也非常高效，但堆排序因其可靠性而被广泛使用。堆排序的关键优势是时间复杂度上限为O(nlogn)，无论是在平均情况还是在最坏情况下。

堆排序算法在平均和最坏情况下都需要O(nlogn)的时间，而快速排序在平均情况下比较快，快20%。

快速排序算法在可预测的情况下变得较慢。在快速排序中，存在触发糟糕O(n2)的机会，从而导致安全漏洞。

现在，我们将其与归并排序进行比较，归并排序所需的时间与堆排序相同。

归并排序更稳定，更容易并行化，而堆排序没有这些优势。

此外，在大多数情况下，归并排序比堆排序更快，因为它们具有相同的时间复杂性。

相反，堆排序可以在原地更快地实现，而归并排序不行。

结论

堆排序并不如其他排序算法那么流行和快速，但它比其他排序算法更可预测。在需要关注内存和安全性的情况下，可以使用此算法。

在Python中可以很快地实现它。我们只需将元素插入堆中，然后取出它们。