SciPy 教程-SciPy 空间

scipy.spatial 包能够通过利用 Qhull 库计算一组点的三角剖分、Voronoi图和凸包。同样，它包含了用于最近邻点查询的 KDTree 实现，以及在各种度量中计算距离的工具。

• Delaunay三角剖分

在数学和计算几何中，Delaunay三角剖分定义了，三个点从三角形中创建一个顶点，当这些顶点接触到圆的路径时。

圆的中心由三个点或三角形的半径决定。让我们考虑以下示例：

from scipy.spatial import Delaunay  
import numpy as np  
import matplotlib.pyplot as plt  
points = np.array([[0, 3], [1, 1.1], [1, 4], [1, 2]])  
triang = Delaunay(points)  
plt.triplot(points[:,0], points[:,1], triang.simplices.copy())  
plt.plot(points[:,0], points[:,1], 'o')  
plt.show()  

输出:

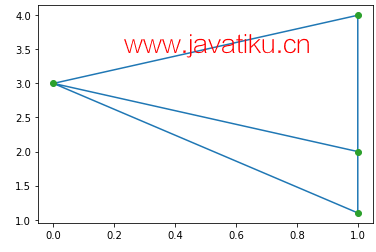
共面点

共面点是指三个或更多点存在于同一平面中。平面是一个可以无限延伸的平坦表面。让我们考虑以下示例：

from scipy.spatial import Delaunay  
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1],[1,1]])  
tri = Delaunay(points)  
print(tri.coplanar)  

输出:

[[4 0 3]]

在上述输出中，点4没有包含在三角剖分中；它存在于三角形0和顶点3附近。

凸包

在数学中，一组点X在欧几里得平面或欧几里得空间中的凸包或凸包络，是包含X的最小凸集。让我们考虑以下示例：

from scipy.spatial import ConvexHull  
import matplotlib.pyplot as plt  
points = np.random.rand(10, 2) # 30 random points in 2-D  
hull = ConvexHull(points)  
plt.plot(points[:,0], points[:,1], 'o')  
for simplex in hull.simplices:  
    plt.plot(points[simplex,0], points[simplex,1], 'k-')  
plt.show()    

输出:

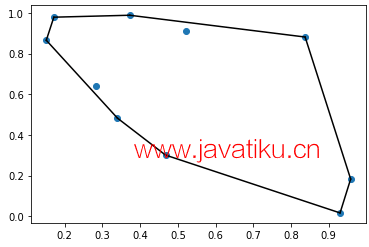
Scipy cdist

SciPy提供了spatial.distance.cdist，用于计算两组输入之间每对点的距离。以下是调用惯例：

1. Y = cdist(XA, XB, 'euclidean')

它使用欧几里得距离（2-范数）计算m个点之间的距离。这些点在矩阵X中被组织为m个n维行向量。

2. Y = cdist(XA, XB, 'minkowski', p=2.)

它使用闵可夫斯基距离 ||u-v||p（p-范数）来计算距离，其中p≥1。

3. Y = cdist(XA, XB, 'cityblock')

它计算点之间的城市区块或曼哈顿距离。