SciPy 教程-SciPy Optimize

SciPy优化包提供了多种常用的优化算法。这个模块包含以下方面：

• 全局优化程序（暴力搜索，anneal()，盆地跳跃）
• 使用多种算法（BFGS，Nelders-Mead单纯形，牛顿共轭梯度，COBLYA）对多变量标量函数进行无约束和约束最小化（minimize()）。
• 最小二乘最小化算法（leastsq()和曲线拟合()）
• 标量单变量函数最小化器（minimizer_scalar()和根查找器newton()）

Nelder-Mead单纯形算法

Nelder-Mead单纯形算法提供了minimize()函数，用于最小化一个或多个变量的标量函数。

import numpy as np  
import scipy  
from scipy.optimize import minimize  
#define function f(x)  
def f(x):     
    return .2*(1 - x[0])**2  
scipy.optimize.minimize(f, [2, -1], method="Nelder-Mead")  

输出:

final_simplex: (array([[ 1.        , -1.27109375],
       [ 1.        , -1.27118835],
       [ 1.        , -1.27113762]]), array([0., 0., 0.]))
           fun: 0.0
       message: 'Optimization terminated successfully.'
          nfev: 147
           nit: 69
        status: 0
       success: True
             x: array([ 1.        , -1.27109375])

最小二乘法最小化

它用于解决具有变量界限的非线性最小二乘问题。给定残差（观测值和预测值的差异）f(x)（n维实函数的n个实变量）和损失函数rho(s)（一个标量函数），least_square找到成本函数f(x)的局部最小值。考虑以下示例：

from scipy.optimize import least_squares  
import numpy as np  
input = np.array([2, 2])  
def rosenbrock(x):  
   return np.array([10 * (x[1] - x[0]**3), (1 - x[0])])  
res = least_squares(rosenbrock, input)  
print(res)  

输出:

active_mask: array([0., 0.])
        cost: 0.0
         fun: array([0., 0.])
        grad: array([0., 0.])
         jac: array([[-30.00000045,  10.        ],
       [ -1.        ,   0.        ]])
     message: '`gtol` termination condition is satisfied.'
        nfev: 4
        njev: 4
  optimality: 0.0
      status: 1
     success: True
           x: array([1., 1.])

寻找根

• 标量函数

对于单值方程，有四种不同的根查找算法。每种算法都需要一个区间的端点，在该区间中预期存在根（因为函数符号变化）。

• 方程组

root()函数用于找到非线性方程的根。有多种方法，例如hybr（默认）和MINPACK的Levenberg-Marquardt方法。

考虑以下方程

x2 + 3cos(x)=0

import numpy as np  
from scipy.optimize import root  
def func(x):  
   return x*2 +  3* np.cos(x)  
a = root(func, 0.3)  
print(a)  

输出:

fjac: array([[-1.]])
  fun: array([2.22044605e-16])
 message: 'The solution converged.'
    nfev: 10
     qtf: array([-1.19788401e-10])
       r: array([-4.37742564])
  status: 1
 success: True

曲线拟合优化

曲线拟合是创建曲线的技术。它是一个数学函数，最适合一系列数据点，可能受到约束。以下是一个示例：

import numpy as np   
from scipy.optimize import curve_fit   
from matplotlib import pyplot as plt   
x = np.linspace(0, 10, num = 40)   
# The coefficients are much bigger.   
y = 10.35 * np.sin(5.330 * x) + np.random.normal(size = 40)   
def test(x, a, b):   
    return a * np.sin(b * x)   
param, param_cov = curve_fit(test, x, y)   
print("Sine funcion coefficients:")   
print(param)   
print("Covariance of coefficients:")   
print(param_cov)   
ans = (param[0]*(np.sin(param[1]*x)))   
plt.plot(x, y, 'o', color ='red', label ="data")   
plt.plot(x, ans, '--', color ='blue', label ="optimized data")   
plt.legend()   
plt.show()  

输出:

Sine funcion coefficients:
[-0.42111847  1.03945217]
Covariance of coefficients:
[[3.03920718 0.05918002]
 [0.05918002 0.43566354]]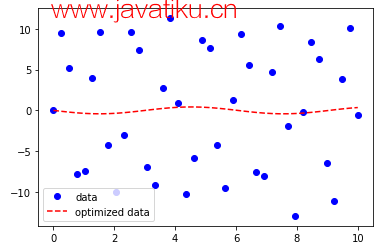

SciPy fsolve

scipy.optimize库提供了fsolve()函数，用于寻找函数的根。它返回由fun(x) = 0定义的方程的根，给定一个起始估计。

考虑以下示例：

import numpy as np  
from scipy.optimize import fsolve  
sqrt = np.emath.sqrt  
a = 132712000000  
T = 365.35 * 86337 * 2 / 3  
e = 580.2392124070273  
def f(x):  
    return np.abs((T * a ** 2 / (2 * np.pi)) ** (1 / 3) * sqrt(1 - x ** 2)  
        - sqrt(.5 * a ** 2 / e * (1 - x ** 2)))  
x = fsolve(f, 0.01)  
x, f(x)  

输出:

(array([1.]), array([82.17252895]))