我们的下一个任务是使用先前标记的图像来训练神经网络，以对新的测试图像进行分类。因此，我们将使用nn模块来构建我们的神经网络。

实现图像识别神经网络的步骤如下：

步骤1：

在第一步中，我们将定义一个类，该类将用于创建我们的神经模型实例。这个类将继承自nn模块，因此我们首先需要导入nn包。

from torch import nn   
class classifier (nn.Module):

我们的类后面将是一个init()方法。在init()中，第一个参数将始终是self，第二个参数将是我们将称为输入节点数的输入层节点数，第三个参数将是隐藏层的节点数，第四个参数将是第二隐藏层的节点数，最后一个参数将是输出层的节点数。

def __init__(self,input_layer,hidden_layer1,hidden_layer2,output_layer):

步骤2：

在第二步中，我们调用init()方法以提供各种方法和属性，并初始化输入层、隐藏层和输出层。请记住，我们将处理全连接的神经网络。

super(),__init__()  
self.linear1=nn.Linear(input_layer,hidden_layer1)  
self.linear2=nn.Linear(hidden_layer1,hidden_layer2)  
self.linear3=nn.Linear(hidden_layer2,output_layer)   
def __init__(self,input_layer,hidden_layer1,hidden_layer2,output_layer):

步骤3：

现在，我们将进行预测，但在此之前，我们将导入torch.nn.functional包，然后我们将使用forward()函数，并将self作为第一个参数，x作为我们尝试进行预测的任何输入。

import torch.nn.functional as func  
def forward(self,x):

现在，传递给forward()函数的任何输入将传递给linear1对象，我们将使用relu函数而不是sigmoid。这个输出将作为输入传递到我们的第二隐藏层，并且第二隐藏层的输出将馈送到输出层，并返回最终层的输出。

注意：如果我们处理的是多类别数据集，就不会在输出层应用任何激活函数。

x=func.relu(self.linear1(x))  
x=func.relu(self.linear2(x))  
x=self.linear3(x)  
return x

步骤4：

在下一步中，我们将设置我们的模型构造函数。根据我们的初始化器，我们必须设置输入维度、隐藏层维度和输出维度。

图像的像素强度将馈送到我们的输入层。由于每个图像都是28*28像素，总共有784个像素，将其馈送到我们的神经网络中。因此，我们将784作为第一个参数传递，我们将在第一和第二隐藏层中分别取125和60个节点，在输出层中我们将取十个节点。

model=classification1(784,125,65,10)

步骤5：

现在，我们将定义我们的损失函数。nn.CrossEntropyLoss() 用于多类别分类。该函数是log_softmax()函数和NLLLoss()函数的组合，NLLLoss是负对数似然损失。对于具有n个类别的任何训练和分类问题，都使用交叉熵。因此，它使用对数概率，因此我们传递行输出而不是softmax激活函数的输出。

criteron=nn.CrossEntropyLoss()

之后，我们将使用熟悉的优化器，即Adam。

optimizer=torch.optim.Adam(model.parameters(),lr=0.001)

步骤6：

在接下来的步骤中，我们将指定epoch的数量。我们初始化epoch的数量并在每个epoch分析损失。我们将初始化两个列表，即loss_history和correct_history。

loss_history=[]  
correct_history=[]

步骤7：

我们将从迭代每个epoch开始，对于每个epoch，我们必须迭代由训练加载器提供的每个训练批次。每个训练批次包含一百个图像以及在train加载器中训练的一百个标签。

for e in range(epochs):  
    for input, labels in training_loader:

步骤8：

当我们迭代图像的批次时，我们必须将它们展平，并使用view方法进行形状变换。

注意： 每个图像张量的形状是（1，28，28），这意味着总共有784个像素。

根据神经网络的结构，我们的输入值将与连接输入层和第一隐藏层的权重矩阵相乘。为了进行这个乘法，我们必须使我们的图像变为一维。我们需要将每个图像从28行2列展平为784个像素的单行。

inputs=input.view(input.shape[0],-1)

现在，借助这些输入，我们得到输出。

outputs=model(inputs)

步骤9：

借助输出，我们将计算总分类交叉熵损失，并最终将输出与实际标签进行比较。我们还将基于交叉熵标准确定错误。在执行训练传递的任何部分之前，我们必须像之前一样设置优化器。

loss1=criteron(outputs,labels)  
optimizer.zero_grad()  
loss1.backward()  
optimizer.step()

步骤10：

为了跟踪每个epoch的损失，我们将初始化一个变量loss，即running_loss。对于计算出的每个批次的每个损失，我们必须将其添加到每个单一批次的所有批次中，然后在每个epoch计算出最终损失。

loss+=loss1.item()

现在，我们将将这个累积的整个epoch的损失附加到我们的损失列表中。为此，在循环语句之后使用else语句。因此，一旦for循环结束，那么将调用else语句。在这个else语句中，我们将打印在特定epoch计算的整个数据集的累积损失。

epoch_loss=loss/len(training_loader)  
loss_history.append(epoch_loss)

步骤11：

在接下来的步骤中，我们将找到网络的准确性。我们将初始化正确的变量并赋值为零。我们将比较模型对每个训练图像的预测与图像的实际标签，以显示在一个epoch中有多少个预测是正确的。

对于每个图像，我们将取得最大分数值。在这种情况下，将返回一个元组。它返回的第一个值是实际的顶值-模型为该批次内的每个单一图像制作的最大分数。因此，我们对第一个元组值不感兴趣，第二个将对应于模型制作的最高预测，我们将其称为preds。它将返回该图像的最大值的索引。

_,preds=torch.max(outputs,1)

步骤12：

每个图像输出将是一个值的集合，其索引范围从0到9，因为MNIST数据集包含从0到9的类。因此，最大值发生的位置对应于模型做出的预测。我们将比较模型对图像的所有这些预测与图像的实际标签，以查看它们中有多少个是正确的。

correct+=torch.sum(preds==labels.data)

这将给出每个图像批次的正确预测数量。我们将以与epoch损失和准确性相同的方式定义epoch准确性，并打印epoch损失和准确性。

epoch_acc=correct.float()/len(training_loader)    
print('training_loss:{:.4f},{:.4f}'.format(epoch_loss,epoch_acc.item()))

这将产生预期的结果，如下所示：

4-1.png

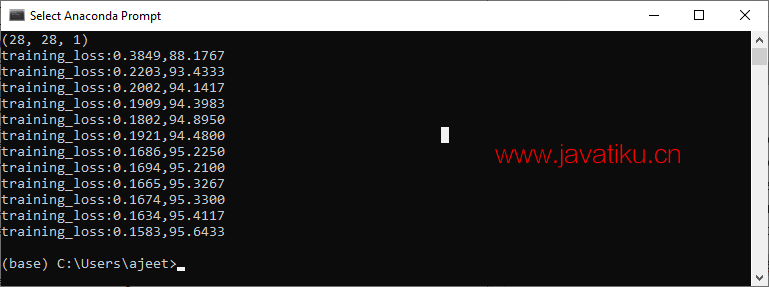
步骤13：

现在，我们将将整个epoch的准确性附加到我们的correct_history列表中，并为更好的可视化，我们将绘制epoch损失和准确性。

plt.plot(loss_history,label='Running Loss History')  
plt.plot(correct_history,label='Running correct History')

Epoch Loss

4-2.png

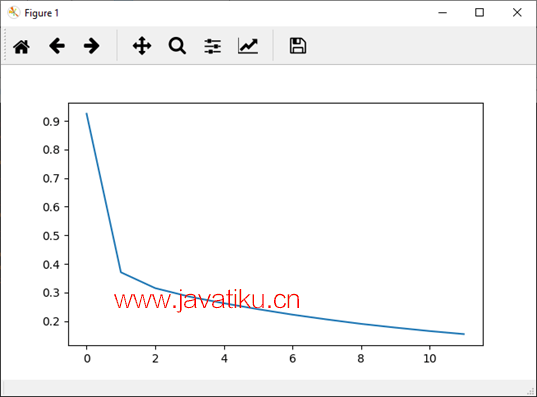
Epoch accuracy

4-3.png

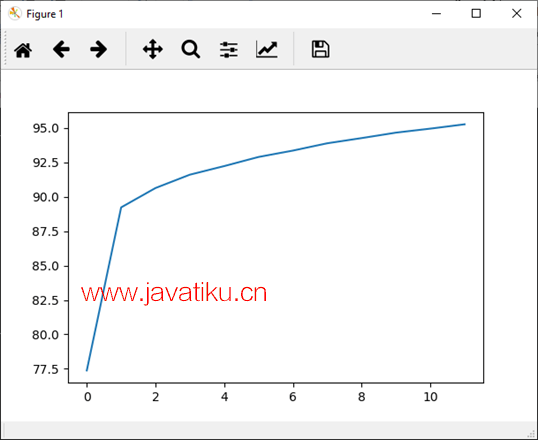
完整代码

import torch  
import matplotlib.pyplot as plt  
import numpy as np  
import torch.nn.functional as func  
from torch import nn  
from torchvision import datasets, transforms  
  
transform1=transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,),(0.5,))])  
training_dataset=datasets.MNIST(root='./data',train=True,download=True,transform=transform1)  
training_loader=torch.utils.data.DataLoader(dataset=training_dataset,batch_size=100,shuffle=True)  
def im_convert(tensor):  
    image=tensor.clone().detach().numpy()  
    image=image.transpose(1,2,0)  
    print(image.shape)  
    image=image*(np.array((0.5,0.5,0.5))+np.array((0.5,0.5,0.5)))  
    image=image.clip(0,1)  
    return image  
dataiter=iter(training_loader)  
images,labels=dataiter.next()  
fig=plt.figure(figsize=(25,4))  
for idx in np.arange(20):  
    ax=fig.add_subplot(2,10,idx+1)  
    plt.imshow(im_convert(images[idx]))  
    ax.set_title([labels[idx].item()])  
class classification1(nn.Module):  
    def __init__(self,input_layer,hidden_layer1,hidden_layer2,output_layer):  
        super().__init__()  
        self.linear1=nn.Linear(input_layer,hidden_layer1)  
        self.linear2=nn.Linear(hidden_layer1,hidden_layer2)  
        self.linear3=nn.Linear(hidden_layer2,output_layer)  
    def forward(self,x):  
        x=func.relu(self.linear1(x))  
        x=func.relu(self.linear2(x))  
        x=self.linear3(x)  
        return x  
model=classification1(784,125,65,10)  
criteron=nn.CrossEntropyLoss()  
optimizer=torch.optim.Adam(model.parameters(),lr=0.0001)  
epochs=12  
loss_history=[]  
correct_history=[]  
for e in range(epochs):  
    loss=0.0  
    correct=0.0  
    for input,labels in training_loader:  
        inputs=input.view(input.shape[0],-1)  
        outputs=model(inputs)  
        loss1=criteron(outputs,labels)  
        optimizer.zero_grad()  
        loss1.backward()  
        optimizer.step()  
        _,preds=torch.max(outputs,1)  
        loss+=loss1.item()  
        correct+=torch.sum(preds==labels.data)  
    else:  
        epoch_loss=loss/len(training_loader)  
        epoch_acc=correct.float()/len(training_loader)  
        loss_history.append(epoch_loss)  
        correct_history.append(epoch_acc)  
        print('training_loss:{:.4f},{:.4f}'.format(epoch_loss,epoch_acc.item()))

标签: Pytorch, Pytorch教程, Pytorch安装, Pytorch入门, Pytorch下载, Pytorch指南, Pytorch编程, Pytorch入门教程, Pytorch初级教程, Pytorch进阶, Pytorch高级教程, Pytorch学习, Pytorch库